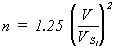For information on Recreational Boating Schools, visit the RBS website.
Table of Contents
- Introduction
- Definitions
- 1. Application
- 2. Construction and Structural Strength
- 3. Stability
- 4. Freeboard and Freeboard Marking
- 5. Watertight & Watertight Integrity
- 6. Water Freeing Arrangements
- 7. Bilge Systems
- 8. Fluid Systems
- 9. Machinery
- 10. Electrical Systems
- 11. Steering Gear
- 12. Fire Safety
- 13. Life Saving and Emergency Equipment
- 14. Communication Equipment
- 15. Navigation Equipment
- 16. Anchors and Cables
- 17. Miscellaneous Marine Equipment
- 18. Accommodation
- 19. Protection of Personnel
- Appendix A: Sample Stability Information Booklet
- Section 1: Operational Information
- Section 2: Technical Data and Loading Conditions
- Section 3: Reference Information
Introduction
The following Standard has been developed to address safety issues pertaining to Canadian mono-hulled sailing vessels engaged in sail training activities at sea. The application of provisions herein is not intended for sailing schools providing instruction in sailing and seamanship to yachtsmen.
Current standards and regulations for conventional ships are not relevant to all areas of the design, construction and operational safety of sail training ships. It was thus deemed necessary to create a standard which would address the particularities of this type of vessel.
The Standard incorporates extensive work and research carried out by numerous administrations including the Marine Directorate of the Department of Transport in the U.K. The feedback obtained from stakeholders throughout the development of this Standard has also contributed significantly to its content.
Definitions
In this Standard:
"Accommodation" includes any space below the weather deck, to which persons on board have access for purposes other than working the ship. This includes messing, sleeping and head spaces, galleys and food stores; it does not include sail or ship's gear lockers.
"Crew" a person other than a trainee or the Master engaged in the business of the ship.
"Existing sail training ship" means any sail training ship which is not a new sail training ship.
"Flame Retardant" when applied to a material means that the material will not burn for more than a specified period of time nor will the flame travel nor extend beyond a specified distance, as determined under certain test conditions at normal atmospheric pressure.
"Freeboard" means the distance in metres measured vertically downwards from the lowest point of the upper edge of the Weather Deck to the waterline in still water.
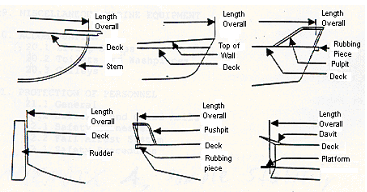
" L " or "Length" means the overall length in metres measured from the foreside of the foremost fixed permanent structure to the aftside of the aftermost fixed permanent structure of the ship.
Figure 1: Definition of Length (Overall)
"Length on the waterline" ( LWL ) means the horizontal distance between the forward-most and after-most points measured at the waterline corresponding to the deepest operational draught.
"New sail training ship" means any ship intended to be used as a sail training ship, the keel of which was laid or constructed or lay-up was started on or after the date of implementation of this standard, or an existing ship obtained and newly used as a sail training ship on or after that date.
"Sail Training Ship", means a sailing vessel which at the time is being operated exclusively for the purpose of providing instruction through a sail training program. Synonymous with the term "Sail Training Vessel".
"Sail Training Program" means a program undertaken aboard a sailing vessel for the sole purpose of character building and educational experiences through participation. This does not include sailing instruction with the sole purpose of increasing sailing proficiency.
"Trainee" means a person on board a sail training ship specifically for the purpose of participating in a sail training program, who is not a member of the crew. Such a person would not legally be considered a passenger.
"Watertight", in relation to a structure, means the structure is capable of preventing the passage of water through it in any direction, under a head of water up to 75 mm below the weather deck at any point.
"Weather Deck" means the main deck or fixed structure that covers the entire hull above the deepest operating waterline and is exposed to weather and sea.
"Weathertight", in relation to a structure, means the structure is capable of preventing the passage of sea water through it in ordinary sea conditions.
1. Application
1.1 This Standard applies to all Canadian mono-hulled sail training vessels, measuring more than 15 m in length, which are engaged in sea activities on a commercial basis. Ships of smaller dimensions should comply with applicable provisions to the maximum practical extent. In addition to the provisions of this Standard, new ships of 24 length and over and existing ships of 150 tons gross and over, as defined in the International Convention on Load Lines, 1966, operating internationally should comply with the appropriate provisions of this Convention. This would not apply to ships solely navigating the Great Lakes of North America and the River St. Lawrence as far east as a rhumb line drawn from Cap des Rosiers to West Point, Anticosti Island, and, on the north side of Anticosti Island, the meridian of longitude 63 degrees W .
1.2 While this Standard applies to mono hulls, it can be used for other types of sail training vessels.
1.3 It is the responsibility of the owner to ensure that a ship to which this Standard applies is constructed, equipped and maintained in compliance with all provisions where appropriate.
1.4 This Standard does not apply to any ship on board which is any person who meets the definition of "Passenger" in the Canada Shipping Act.
1.5 The owner of a ship should demonstrate to the satisfaction of Transport Canada, Marine Safety Directorate, that each person is required on board to handle the ship under sail and that each person has entered into a contractually binding agreement with the ship owner to serve in some capacity on the ship. Such persons are not legally considered passengers, and ships complying with the above provisions should be considered non-passenger ships.
2. Construction and Structural Strength
2.1 Hulls
2.1.1 All ships should be of adequate structural strength to withstand the sea and weather conditions likely to be encountered in the intended area of operation.
2.1.2 Hull, scantlings, decks and superstructures of a new ship may be constructed of any material acceptable to Transport Canada Inspectors.
2.1.3 An existing ship will be considered to be of adequate structural strength if it is in a good state of repair and is:
- built to the standards prescribed by classification societies acceptable to Transport Canada ( TC ); or
- of a design with a record of at least 5 years safe operation in an area where the sea and weather conditions are no less severe than those likely to be encountered in the intended area of operation.
2.1.4 In constructing metal hulls, due consideration should be given to electrolytic corrosion, and appropriate means of minimizing its effects should be employed. In applying corrosion protection measures, the ship should be deemed to be intended for operation in seawater except if it is to be limited to freshwater operation. In ships with metal hulls, an isolation transformer or a galvanic isolator in the grounding conductor of shore power connection may be considered to reduce galvanic corrosion.
2.2 Weather Deck
2.2.1 The ship should have a weathertight weather deck which extends from stem to stern. The weather deck may be stepped, recessed or raised provided the stepped, recessed or raised portion is of weathertight construction.
2.2.2 Any recess in weather deck should be self-draining under normal conditions of heel and trim and the means of drainage should be capable of efficient operation when the ship is heeled to 30 degrees.
2.3 Watertight Bulkheads and Subdivision
2.3.1 Each ship should be fitted with collision bulkhead and machinery space bulkheads. For ships having small machinery spaces, those spaces may be protected with partial transverse and longitudinal bulkheads forming an enclosure in lieu of the full transverse bulkheads.
2.3.2 The collision bulkhead should be located at a distance of not less than 5% and not more than 10% of the LWL abaft the stem measured at the deepest operational waterline. For ships with a higher rake of stem, the collision bulkhead may be stepped, with the lower part of the bulkhead to step located as above, and the top of the step being not less than 2.5% of LWL above the deepest operational waterline.
2.3.3 Every new ship should be subdivided with watertight bulkheads so arranged that the flooding of any one compartment will not cause the ship to float at waterline which is less than 75 mm below the weather deck at any point. Subdivision analysis should be based on the assumption that the ship is in the maximum loaded condition and be carried out using standard permeabilities as defined in the Hull Construction Regulations.
2.3.4 It is recommended that ships for which 2.3.3 applies, have the residual stability in the final flooded condition after damage such that:
- the angle of equilibrium does not exceed 7 degrees from upright;
- the resulting righting lever curve has a range of at least 15 degrees beyond the angle of equilibrium; and
- the maximum righting lever within the range that is not less than 0.015 metre radians;
2.3.5 It is also recommended that at intermediate stages of flooding the maximum righting lever be at least 50 mm with a range of positive righting levels of at least 7 degrees.
2.3.6 Existing ships having a length of 24 m and above should comply with the provisions given in the section 2.3.3. Ships which do not meet these requirements may be accepted by Marine Safety after an assessment of the deficiencies is made and consideration is given to compensatory measures such as operational limitations.
2.3.7 For existing ships of less than 24 m in length, it is strongly recommended that modifications which would cause the ship to comply with provisions given in the section 2.3.3 be implemented when the ship undergoes major structural alterations.
2.3.8 The provisions given in sections 2.3.3 do not need to apply to ships operating exclusively on minor water voyages as defined in the Home Trade, Inland and Minor Waters Voyages Regulations.
2.3.9 Where pipes, cables etc. penetrate watertight bulkheads they should be fitted with valves and watertight glands as appropriate.
2.3.10 Doorways fitted in watertight bulkheads should be of watertight construction and unless otherwise authorised by the Master, be kept closed while at sea.
2.4 Masts, Spars and Rigging
2.4.1 The design, materials and construction of masts, yards, booms, bowsprits and standing rigging including their supporting structures should be suitable for intended service and should have adequate strength to withstand the highest loadings imposed by the sail system during all normal and emergency operations.
2.4.2 Particular attention should be given to the integration of the masts and rigging into the hull structure. The hull structure should be adequately reinforced and stiffened to ensure sufficient strength and resistance to plate buckling.
2.4.3 All standing rigging should have positively secured ends, and lower terminations should incorporate means of adjustment. Safe, traditional, time proven methods may be acceptable if considered satisfactory to the attending inspector.
2.4.4 All running rigging should be provided with clear running leads, using swivel blocks, fairleads, pad-eyes, etc. as appropriate. All running rigging components should be of adequate design and size to minimize the risk of jamming.
2.4.5 The strength of all blocks, shackles, rigging screws, cleats and associated fittings and attachment points should exceed the breaking strength of associated running and standing rigging.
2.4.6 Every ship should be provided with adequate means of reefing or shortening sails.
2.4.7 Unless clearly unsuitable, every ship should either be provided with separate storm sails of adequate strength and size or have specific sails designated and constructed to act as storm canvas.
2.4.8 Adequate provision should be made for securing running rigging, assuming the simultaneous use of sails.
2.5 Fabrication Standards
2.5.1 Hull construction and maintenance should be carried out in an appropriate environment as prescribed by the manufacturer.
2.5.2 Hulls should be fabricated in facilities equipped as appropriate for the material of construction; materials of construction and any consumables used during fabrication should be stored in such a way as to prevent corrosion or other deterioration, and in compliance with any instructions provided by the manufacturer.
2.5.3 Wooden fabrication of hulls should, to the most complete stage practical, be performed in well ventilated covered premises.
2.5.4 Fibre reinforced plastic fabrication should be carried out in a an environment with atmospheric control to maintain the temperature between 15° and 21 °C ., and relative humidity constant within the range 40%-80% during fabrication.
2.5.5 Welded fabrication should be performed by welders holding appropriate certification in compliance with standards and practices appropriate to the material of construction, welding methods and equipment being used. This provision is not intended to exclude work carried out by a recognised apprentice welder or metal worker under the supervision of a tradesman welder.
2.5.6 All construction other than welding should be performed by persons skilled in the particular method and material of construction.
3. Stability
3.1 Intact Stability
3.1.1 The centre of gravity ( KG ) of the ship should be established by an inclining experiment and curves of statical stability ( GZ curves) calculated for the following conditions:
- b) loaded departure, 100% consumables
- c) loaded arrival, 10% consumables.
3.1.2 For each of the conditions listed in 3.1.1, the righting arms curve should have a positive range of not less than 90 degrees. A minimum positive range of the righting arms curve for a ship of length smaller than 24 m may be determined by the formula:
90° + 25° x (24 - L ) ÷ 9,
however, a positive range of less than 90 degrees may be considered subject to operational limitations.
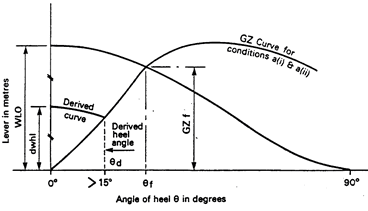
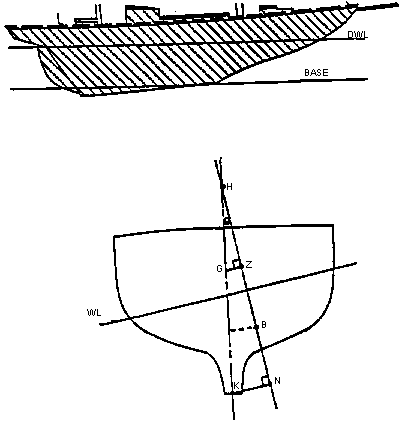
3.1.3 In addition the angle of steady heel obtained from the intersection of a "derived wind heeling lever" curve with either of the GZ curves referred to in sub paragraph 3.1.1 above should be greater than 15 degrees (see Figure 2)
Figure 2: Stability Curves
In Figure 2
‘ dwhl ’ = the "derived wind heeling lever" at any angle Θ degrees.
= 0.5 x WLO x Cos1..3Θ
where WLO = GZf / Cos1..3 Θf
Noting that:
WLO - is the magnitude of the actual wind heeling lever at 0 degrees which would cause the ship to heel to the ‘downflooding angle’ ( Θf or 60 degrees whichever is least).
If the use of some other angle, between the downflooding angle and 40 degrees, would result in a greater value of the maximum steady heel angle, this may be used as an alternative to Θf ,
GZf - is the lever of the ship's GZ curve at the ‘downflooding angle’ ( Θf ) or 60 degrees whichever is least,
Θd - is the angle at which the ‘derived wind heeling’ curve intersects the GZ curve. (If Θd is less than 15 degrees the ship will be considered to have insufficient stability for the purpose of this Standard).
Θf - the ‘downflooding angle’ is deemed to occur when openings having an aggregate area, in square metres, greater than:
ship's displacement in tonnes / 1500
are immersed. Moreover, it is the angle at which the lower edge of the actual opening which results in critical flooding becomes immersed.
3.1.4 All openings regularly used for crew access and for ventilation should be considered when determining the downflooding angle. No opening, regardless of size, which may lead to progressive flooding should be immersed at an angle of heel of less than 40 degrees. Air pipes to tanks can, however, be disregarded.
3.1.5 If as a result of the immersion of openings in a deckhouse a ship cannot meet the required standard, those deckhouse openings may be ignored and the openings in the weather deck protected by this deckhouse may be used instead to determine Θf . In such cases the GZ curve should be derived without the benefit of the buoyancy of the deckhouse.
3.1.6 Provided the ship complies with the requirements of subparagraphs 3.1.1, 3.1.2 and 3.1.3 and that it is sailed with an angle of heel which is no greater than the ‘derived angle of heel’, it should be capable of withstanding a wind gust equal to 1.4 times the actual wind velocity ( i.e. twice the actual wind pressure) without immersing the ‘downflooding openings’, or heeling to an angle greater than 60 degrees.
3.1.7 A ship having a positive range of righting arms smaller than 90 degrees may have its effective range of stability significantly reduced in the event of steadily increasing wind that may lead to capsizing at the angle of heel for which the heeling arms curve becomes tangent to the righting arms curve. Ships with such stability characteristics should have an appropriate warning note included in the stability guidance for the Master.
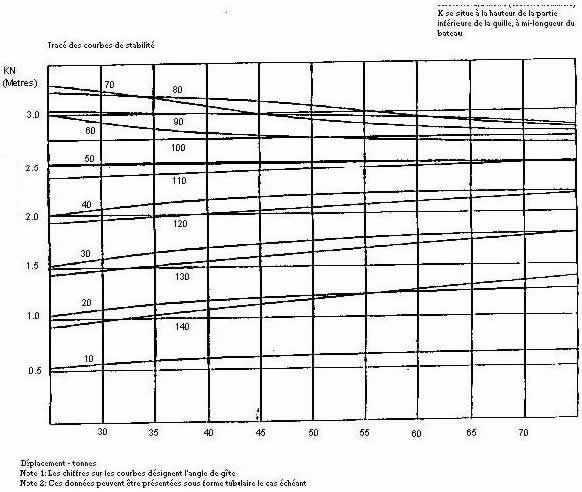
3.2 Stability Information Booklet
3.2.1 A ‘Stability Information Booklet’ with its content, form and presentation based on the model booklet given in Appendix A should be placed on board for the guidance of the master.
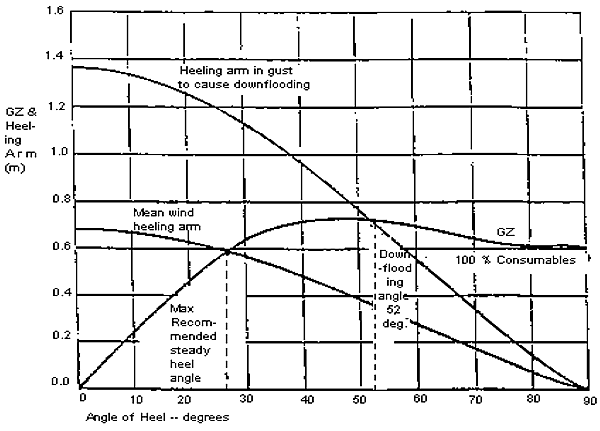
3.2.2 This Booklet should include details of the maximum steady angle of heel for the worst sailing condition which is to be calculated in accordance with subparagraph 3.1.3.
3.2.3 The Booklet should also include curves of maximum recommended steady angle of heel for the prevention of downflooding in the event of squall conditions. Details of the development of such curves are given in Appendix A.
3.2.4 It is recommended that a direct copy of the Curves of Maximum Steady Heel Angle to Prevent Downflooding in Squalls taken from the stability booklet, be mounted on a ship in a suitable position for the ready references of a crew.
3.3 Inclining Experiment
3.3.1 A general description of the experiment should be presented with details of the personnel responsible, prevailing conditions, procedure and equipment used, as well as precautions to be taken to ensure accuracy.
3.3.2 Successful inclining of a sailing ship requires conditions with little or no wind because of significant windage of the rig.
4. Freeboard and Freeboard Marking
4.1 Every ship should have an assigned freeboard mark placed on each side of the hull at amidships at the maximum draught at which the stability of the ship has been determined.
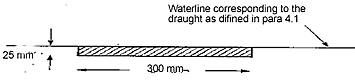
4.2 The freeboard mark referred to above should measure 300 mm in length and 25 mm in depth, as shown in Figure 3. It should be marked in a permanent manner and painted black on a light background or in white or yellow on a dark background. The top of the mark should be positioned at the waterline corresponding to the draught referred to in 4.1.
Figure 3: Freeboard Marking
4.3 The ship should not operate in any condition which will result in its freeboard marks being submerged when it is at rest and upright in calm waters.
5. Watertight & Watertight Integrity
5.1 Decks
All decks exposed to the weather should be watertight, and means should be provided to make any openings weathertight.(see 2.2)
5.2 Hatchways
5.2.1 All hatch openings in the weather deck should be provided with a watertight coaming of not less than 300 mm high. Hatches covering access to deck lockers should be fitted with a means of securing them in the closed position.
5.2.2 Hatches covering normal access to accommodation on working spaces should be operable from both sides and should be fitted with a means of positively securing them in the open and closed position.
5.2.3 It is recommended that hatchways be located on the centre line of the ship or as close thereto as is practical.
5.2.4 It is recommended that in general, hatches be kept closed at sea. It is also recommended that hatchways which are to be kept open for lengthy periods at sea be as small as practical, but never more than 1 metre square in clear area at the top of the coaming.
5.3 Doorways and Companionways
5.3.1 Doorways located above the weather deck which give access to spaces below should be provided with coamings not less than 300 mm high and with weathertight doors.
5.3.2 Such doors should be of efficient construction, permanently and strongly attached to the bulkhead, open outwards and have a means of closure which can be operated from either side.
5.3.3 They should be located as close as practical to the centre line of the ship but if located in the sides of a house, they should be hinged on the forward edge.
5.3.4 Companion hatch openings from a cockpit or recess which give access to spaces below the weather deck should be fitted with a coaming the top of which is at least 300 mm above the sole of the cockpit or recess. The maximum breadth of the opening in a companion hatch should not exceed 1 metre.
5.3.5 On existing vessels where adequate coamings are not fitted, shifting boards should be fitted to a height of 300 mm and have adequate visible adjacent storage.
5.4 Skylights
5.4.1 All skylights should be of weathertight construction and should be located on the centre line of the ship or as near thereto as practical. If they are of the opening type, they should be fitted with a coaming at least 300 mm above the deck and with efficient means of closing.
5.4.2 Any openings in the weather deck designed as skylights should incorporate toughened safety glass or an equivalent of at least 6 mm thickness. They should be provided with portable covers which can be secured in place in the event of breakage.
5.5 Portlights and Windows
5.5.1 Portlights, scuttles and windows to spaces below the weather deck, in a deckhouse or superstructure protecting openings leading below the weather deck should be of efficient construction and fitted with permanently attached deadlights capable of being closed weathertight.
5.5.2 In a new ship a portlight or window should not be fitted in the main hull below the weather deck, unless the glazing material and its method of fixing in the frame are equivalent in strength to that required for the structure in which it is fitted.
5.5.3 In a new ship, a scuttle should not be provided to a space situated below the weather deck.
5.5.4 It is recommended that a scuttle does not exceed 250 mm in diametre or equivalent in size.
5.5.5 If windows are to be fitted in spaces above the weather deck which protect openings leading below the weather deck, they should be of weathertight construction. Portable covers should be provided at the rate of 50% for each size of window, which can be secured weathertight in the event of breakage.
5.5.6 The portlights, scuttles and windows described above should incorporate toughened safety glass or an equivalent of at least 6 mm in thickness.
5.6 Ventilators
5.6.1 Ventilators should be of efficient construction and provided with a permanently attached means of weathertight closure.
5.6.2 Ventilators should be kept as far inboard as practical and have a height to the lower edge of the opening of not less than 915 mm above the weather deck.
5.6.3 Ventilators which must be kept open ( e.g. for the supply of air to machinery or for the discharge of noxious or flammable gases) should be specially considered with respect to their location and height above deck given that they may become downflooding points.
5.6.4 Ventilators should be positioned such that they will not interfere with the safe operation of the vessel or where they can be caused damage by such operations.
5.7 Air Pipes
5.7.1 Air pipes greater than 10 mm inside diametre serving fuel or other tanks should be of efficient construction and be provided with a permanently attached means of weathertight closure. Air pipes should be in accordance with the Marine Machinery Regulations schedule XV Part 1 Div II Sections 78 to 89.
5.7.2 Where located on the weather deck they should extend a minimum of 300 mm above the weatherdeck and be fitted with a gooseneck.
5.8 Sea Inlets and Discharges
5.8.1 All openings below the weather deck should be fitted with an efficient means of closure.
5.8.2 Where the opening is for the purpose of an inlet or discharge below the waterline, it should be fitted with a seacock, valve or other means of closure which is readily accessible in an emergency.
5.8.3 Where the opening is for a log or any other sensor which is capable of being withdrawn, it should be fitted in a watertight manner and provided with an effective means of closure when such a fitting is removed.
6. Water Freeing Arrangements
6.1 Any exposed deck fitted with gunwale or bulwark such that shipped water may be temporarily trapped behind them should be provided with an adequate number of freeing ports.
6.2 The total area of the freeing ports should be at least 10% of that part of the bulwark or gunwale area which extends for 2/3 of the ship's length amidships. A freeing port should be located in the lower third of the gunwale or bulwark height, as close to the deck as practical.
6.3 Freeing ports over 300 mm in depth should be fitted with bars spaced not more than 230 mm apart or other suitable protecting devices. If freeing ports are fitted with shutters, these should be hinged at the top to open outboard. The shutter hinges should have pins or bearings of non-corrosive material.
6.4 Structures and spaces above the weather deck considered to be non-weathertight should be provided with efficient drainage arrangements.
7. Bilge Systems
7.1 Every ship should be equipped with an efficient self priming bilge pumping system consisting of at least:
- For ships of length less than 20 m - one hand bilge pump having a minimum capacity of 1 m3/hr and one engine driven or independent, fixed power bilge pump having a minimum capacity of 5 m3/hr ;
- For ships having length of 20 m and over - two fixed power driven pumps having combined minimum capacity of 10 m3/hr .
7.2 Pumps and piping should be so arranged that any compartment can be drained and that the overhaul of a pump should be possible without putting other bilge pumps out of action.
7.3 For an existing ship which can not meet the requirements given in 7.1 and 7.2 consideration may be given to alternative arrangements to achieve an adequate safety standard.
7.4 Portable pumps should not weigh more than 20 Kg .
7.5 Spaces connected to a permanently installed bilge system should be provided with suctions positioned so as to permit removal of flood water when the ship is heeled to 15 degrees in either direction.
7.6 Bilge pumps connected, or capable of being connected to the bilge system should be capable of efficient operation with the ship heeled to 30 degrees in either direction.
7.7 Permanently installed bilge piping should be arranged so as to prevent the transfer of flood water from one compartment to another.
7.8 All bilge piping should be smooth bore and not less than 25 mm in diametre; suctions should be through strum boxes.
7.9 Portable pumps, their power supply and hoses, should be stowed in clearly marked stowages, secured with quick-release fastenings.
7.10 All bilge suction valves and pump discharge valves in new sail training ships should be of the screw down non return type. Bilge system pipes should be clearly marked as such, and any bilge suction valve controls should be clearly identified with the compartment served.
7.11 Through-hull bilge system discharges should be by way of non-return valves or a syphon valve at the through-hull fitting.
8. Fluid Systems
8.1 All permanently installed tanks provided for containing fluid should be located on the longitudinal centreline or as close thereto as practical, oriented fore and aft, and located as low in the ship as possible. It is recommended that fuel tanks be fitted with divisions / baffles to minimise free surface effect.
8.2 All permanently installed tanks should be securely mounted and fastened to the ship structure, paying due regard to dynamic loads, differential expansion, and electrolytic corrosion.
8.3 The material of tanks and all components of a fluid system should be compatible with the fluid contained, neither being corroded by the fluid nor impairing the quality of the fluid.
8.4 All joints in fluid systems should be positively secured using approved methods appropriate to the material of construction.
8.5 Any components of a fluid system requiring periodic servicing or inspection should be readily accessible to permit ease of performing the required operation.
8.6 Fluid connections to tanks should be provided with valves or cocks to permit isolation of leaks or removal of system components.
8.7 Any component of a fluid system should be designed with a safe working pressure of 1.5 times the normal maximum service pressure, paying due regard to any static head within the system.
8.8 All permanently installed tanks containing replenishable consumables should be provided with identified filling connections and watertight filler caps.
8.9 All permanently installed tanks should be provided with vents in accordance with the Marine Machinery Regulations schedule XV Part 1 Div II Sections 78 to 89.
8.10 Any "grey water" overboard discharges should be by way of through-hull fittings incorporating non-return valves or shut-off cocks.
8.11 All permanently installed fluid or vent piping connected to fuel or sewage tanks should, to the maximum extent practical, be remote from accommodation spaces and normal work stations. All such tank vents should have flame screens of non-corrosive material fitted at the exit.
8.12 All ship service drains should be installed with a minimum fall towards the tank connection of 5% unless fitted with a vacuum system.
9. Machinery
9.1 Internal Combustion Engines
9.1.1 Every new ship should be fitted with a marine diesel engine and a sufficient supply of fuel capable of propelling it in a calm sea at a speed of minimum 6 knots for a period of at least 24 hours. Ships in which engines using other fuels are installed should be subject to special consideration of the Board in respect of fire safety provisions.
9.1.2 All engine seatings and securing arrangements, and their ship supporting structure should take into consideration the loadings arising from an acceleration of 2 g in any direction up to angles of heel of 60 degrees.
9.1.3 The design of any engine, and the installation arrangement in the ship should permit unrestricted operation at angles of heel up to 15 degrees. All machinery should be designed to operate when the ship is upright and when listing at any angle up to and including 15 degrees either way under static conditions and 22.5 degrees either way under rolling conditions and simultaneously inclined 7.5 degrees by the bow or stern under pitching conditions
9.1.4 Installation of engines should permit full and ready access to all replenishment points, system connections valves, and filters.
9.1.5 All fluid system connections to engines should be provided with cocks or valves on the hull side, to permit removal of the engine.
9.1.6 Space beneath the engine should be arranged so as to contain any leakage of fluid, and to provide adequate access for removal of such fluid accumulation.
9.1.7 Installation of engines should ensure unrestricted supply of cooling fluids and combustion air in accordance with the engine manufacturer's recommendations.
9.1.8 Combustion and cooling air should be ducted from the weather deck, such ducts being arranged so as to minimize the ingestion of spray or moisture.
9.1.9 Ventilation and cooling airflow should be provided by separate ducts, with equal cross-section area provided for intake and exhaust. Where combustion air is drawn from within the machinery space, the intake duct cross-section area should be proportionally increased.
9.1.10 All ventilation and combustion air ducting should be adequately supported and so far as practical should not pass through any accommodation space.
9.1.11 The cross sectional area of inlet ducts and of exhaust ducts providing ventilation/cooling air only should be at least 22 sq.cm. for each metre of ship beam .
9.1.12 Each engine should be provided with a means of speed control and stopping. Instrumentation should be provided at the position from which the engine is normally controlled, monitoring such parametres and marked with any manufacturer's limitations as recommended by the engine manufacturers. Visual and audio warnings should be provided in the event that fault conditions leading to engine failure develop.
9.1.13 Engines which are normally monitored and controlled from a remote station should be provided with local means of control and monitoring.
9.1.14 Moving parts, hot surfaces and other hazards should be so installed and protected as to minimise any danger to persons on board.
9.1.15 Exhaust pipe runs should be as short as practical and any penetration of partitions or of the ship hull should be adequately insulated. No dry exhaust pipes should be run through spaces normally used for accommodation.
9.1.16 No dry exhaust pipe should terminate within 1 metre of the weather deck, a ventilation intake or a survival craft.
9.1.17 Provision should be made for two-way communication between spaces containing propulsion engines and the station from which the ship is normally steered except if considered impractical by the attending surveyor.
9.1.18 All permanently installed engines should be capable of being started from a "dead ship" condition while alongside.
9.1.19 Engines used for ship propulsion should be installed in enclosed spaces, which should to the maximum extent practical be watertight and any bulkhead common with an accommodation space should be fire resistant and vapour-proof.(see 12.4.8)
9.1.20 Any electrical equipment installed in an enclosed machinery space should be of a certified safe or intrinsically safe type for use in the dangerous environment to which the equipment may be exposed.
9.2 Transmission and Shafting
9.2.1 Engine power for propulsion should be transmitted through transmission and shafting designed and installed in compliance with TC accepted classification society rules or should be of a design with a record of at least 5 years safe operation in similar installation.
9.2.2 Transmissions should provide for ahead and astern propulsion including neutral mode.
9.2.3 Transmission control should be adjacent to controls for the connected engine.
9.2.4 No shafting should penetrate accommodation spaces.
9.2.5 Shafting should be designed and installed so as to ensure that first order critical (whirling) speed is not less than 110% of the maximum designed operating speed.
9.2.6 Shaft penetrations of the hull should be by way of stern glands and bearings in accordance with established practice and provided with the appropriate adjustment or system for lubrication.
10. Electrical Systems
10.1 General
10.1.1 Electrical arrangements should be such as to minimise risk of fire and electric shock. Particular attention should be paid to the provision of overload and short circuit protection of all circuits, except engine starting circuits, which are battery powered.
10.1.2 Where general lighting within the ship is provided by a centralised electrical system, an alternative source of lighting ( e.g. battery operated escape lights sufficient to enable persons to make their way up to the open deck) should be provided.
10.1.3 Electrical components and cables and wires of systems of dissimilar electrical characteristics should be kept separate to the maximum extent practical, and voltage characteristics should be identified at origination or the destination of the circuit.
10.1.4 All cables, connectors and terminations should be sized paying due regard to their current carrying capacities; all cables carrying less than 55 volts should have stranded copper conductors, flame retardant insulation and be of a suitable commercial grade rated for at least 75 °C service. For cables carrying over 55 volts, TC approved marine cable should be employed.
10.1.5 All electrical circuits should be provided with individual protection from the effects of overcurrent by suitable rated fuses or circuit breakers; both AC and DC circuit breakers should be of manual re-setting "trip free" type.
10.1.6 All electrical components and cabling exposed to the weather should be waterproof and of non-corrosive material. Any cable penetrations of ship structure on the weather deck should be by way of watertight connections.
10.1.7 Any electrical power supplies to navigation lights, steering systems or battery charging should include indication visible to the control point in the event that supply has failed.
10.1.8 The function of all switches, fuses and circuit breakers should be identified.
10.1.9 The cabinets or enclosures of all radios and electronic devices, fuel tanks and fuel filling connections should be bonded to a bonding system which is connected to the negative side of the electrical system. All bonding conductors should be copper or bronze.
10.1.10 Electrical wiring routing should, to the maximum possible extent, avoid any compass or compass system component. Where such a routing is unavoidable, D.C. wiring should be run in twisted pairs and be installed following compass manufacturers’ recommendations.
10.1.11 Lightning conductors should be fitted to each mast of non-metallic ships and to each mast of steel or aluminium ships having wooden masts or topmasts except where the height of any antenna exceeds that of the masts and the antenna is equipped with lightning arrestors or other effective devices.
10.1.12 Lightning conductors should be composed of continuous copper tape or cable having a cross sectional area of not less than 25 mm² (#4 AWG ) and should be continuous from a point 150 mm above the mast truck to a copper plate of not less than 0.2 m² in area fixed to the keel below the waterline in a manner that it remains immersed under all conditions of heel and trim; the lightning conductor plate should only be used for lightning conductor purposes.
10.2 D.C. Systems
10.2.1 D.C. systems should be of a two-wire type with insulated feed and return; systems of more than 55 Volts should be in accordance with TP 127.
10.2.2 Provided that engines installed in metallic-hulled ships are electrically isolated from the hull, all engine blocks may be used as a common ground return for engine-mounted electrical equipment.
10.2.3 Non-conducting exposed metal parts of electrical equipment should be grounded to the hull; in ships of wooden or reinforced plastic hull construction, this grounding should be by way of a continuous conductor terminating on the main engine or a copper ground plate of area not less than 0.2 m² fixed to the keel below the light waterline so as to be fully immersed under all conditions of heel.
10.2.4 All grounding connections should be of copper, readily accessible and securely fastened and protected as necessary against damage and electrolytic corrosion.
10.2.5 In grounded distribution systems, the grounded side should be of negative polarity.
10.2.6 Distribution panels and switchboards should be located in well-ventilated areas protected from rain or spray which may enter through scuttles, vents or deck openings.
10.2.7 The D.C. switchboard or distribution panel should include a voltmetre, an ammetre as well as an indicator of battery charging.
10.2.8 The D.C. switchboard or distribution panel should also provide indication of ship circuits to which power is connected. This may be by way of switches incorporating indicating lights.
10.3 Battery Storage
10.3.1 Battery storage facilities are to be well labelled and indicate the hazard contained within.
10.3.2 Every battery as installed should not move more than 25 mm when a pulling force of 40 kg or twice the battery weight, whichever is less, is applied through the centre of gravity, in each of the following five directions for one minute:
- vertically;
- horizontally, fore and aft; and
- horizontally, to port and starboard.
10.3.3 No battery should be installed directly above or below a fuel tank, fuel filter or fuel line fitting.
10.3.4 Batteries should not be installed in accommodation spaces, or spaces containing flammable stores. It is recommended that batteries not be installed in machinery spaces unless adequate arrangements are made for the dispersion of exhaust gases generated by charging; it is also recommended that batteries provided for engine starting purposes be installed adjacent to the engine, to reduce the length of conductors.
10.3.5 Every metallic fuel line and fuel system component above the level of the top of an installed battery should be shielded with dielectric material.
10.3.6 No battery should be installed such that metallic objects can come in contact with the ungrounded battery terminals.
10.3.7 Batteries of different types of construction, or using different electrolytes, should be secured in separate stowages.
10.3.8 The positive terminal of a battery should be identified on the terminal or on the battery case near the terminal with one of the following symbols:
- ‘POS’;
- ‘P’; or
- ‘+’ .
10.3.9 No battery terminal connector should depend upon spring tension for its connection to the terminal.
10.3.10 Vented batteries connected to a charging device with a power output of more than 2 KW are to be housed in an adequately ventilated compartment assigned to batteries only, or may be installed in a suitable box on deck.
10.3.11 Vented batteries connected to a charging device with a power output within a range of 0.2 KW to 2 KW are to be installed in accordance with 10.3.10, or may be installed in a box within a well vented machinery or similar space.
10.3.12 The interiors of all compartments for vented batteries, including crates, trays, boxes, shelves and other structural parts therein are to be of a corrosion resistant material and if necessary covered with a suitable paint or lining material.
10.3.13 Battery compartments and boxes should be provided with ventilation in accordance with subsection 10.3.14 to prevent accumulation of dangerous flammable gasses which may occur during the charging and discharging processes and due consideration should be given to the protection of the battery (batteries) from environmental conditions.
10.3.14 Natural ventilation may be provided for batteries if ducts can be run directly from the top of the compartment or box to the open air above, with no part of the duct inclined more than 45° from the vertical; if natural ventilation is impractical, mechanical exhaust ventilation for vented batteries should be provided where the quantity of air expelled is at least equal to:
Q = 110×I×N
Where :
N = number of cells in series
I = maximum current delivered to the charging equipment during gas formation, but not less than 25% of the maximum obtainable current in amperes
Q = quantity of air expelled in litres/hr
10.3.15 All batteries permanently connected to the ship's electrical systems should be provided with a charging circuit, which should include arrangements to prevent reversed polarity of the charging circuit and to prevent battery discharge through the charging circuit.
10.3.16 Any permanently installed batteries which may experience thermal runaway should be equipped with a temperature warning device which activates a distinctive audible warning. The charging circuits should be provided with isolating switches or circuit breakers.
10.3.17 Battery isolator switches should be provided to disconnect all permanently installed batteries from the ship's distribution system.
10.4 A.C. Systems
10.4.1 Preferred system characteristics, to which this standard refers, are 120 V , 60 Hz , single phase 2-wire insulated system, 120/240 V , 60 hz , single phase 3-wire with grounded neutral or 3 phase, 3-wire ungrounded system.
10.4.2 The system should be polarized and conductors should be uniformly identified:
- insulated ground conductors = green;
- ungrounded conductors = black and/or red
- neutral = white.
10.4.3 Grounding conductors should be connected to the ground at only one point, the main distribution switchboard (panel).
10.4.4 Circuit design should ensure that no circuit may be fed simultaneously by more than one power source.
10.4.5 Any connector for the supply of shore power should be of weathertight design.
10.4.6 The power feed cable from a shore connection to the switchboard or distribution panel should have a circuit breaker or fused disconnected switch located not more than 3 m inboard of the shore connection. A polarity indicator for DC or single phase AC systems or a three phase sequence indicator should be fitted at the shore receptacle or on the switchboard.
10.4.7 All power feed conductors, from on-board generators or shore connection should be provided with over-current protection by common trip circuit breakers as follows:
- 120 V single phase - both ungrounded conductors.
- 120/240 V and 240 V single phase - both ungrounded conductors;
- 120/240 or 120/208 V three-phase - all ungrounded conductors.
10.4.8 Each branch circuit operating at voltages of 55 volts or over should be provided with a switch or circuit breaker with a pole for each conductor; any switch or circuit breaker fitted should operate simultaneously in the grounded conductor and the insulated conductor.
10.4.9 All fuses or circuit breakers should be rated so as not to exceed the current rating of the smallest connected conductor; motors should be protected by devices which are responsive to motor current.
10.4.10 On a grounded neutral distribution system ground fault circuit interrupters may be used on single-phase circuits to protect personnel and equipment; ground fault protectors may be used to protect equipment.
10.4.11 Transformers should be protected from short circuit on the primary side, and protected from overload by devices either installed on the primary or secondary side set or rated less than 125% of their respective currents.
10.4.12 The two wire branch circuit should not supply points which exceed 80% of the set value of the branch circuit protection device.
10.4.13 The AC switchboard or distribution panel should be provided with instrumentation indicating generator voltage and current to indicate the state of insulation to ground.
10.4.14 All systems of 120 V and above should have cable insulation resistance tests carried out upon completion of installation.
10.5 Emergency Power Supply
10.5.1 In every ship, battery capacity should be sufficient to power the following equipment simultaneously for 12 hours;
- Emergency lighting on the weather deck at survival craft deployment and embarkation points;
- Emergency lighting at each exit used as a primary means of escape to the weather deck;
- Compass illumination;
- One radio transceiver, assuming a total accumulation of 30 minutes transmission;
- Any fire detection or extinguishing system which relies on electrical power for its effectiveness.
- Where required by the collision regulations, the electrical supply to the navigation light panel.
In the case of a ship engaged regularly on voyages of short duration, a lesser period than 12 hours specified above may be allowed.
10.5.2 Any of the requirements of 10.5.1 may be satisfied by local batteries subject to suitable arrangements to ensure their condition.
11. Steering Gear
11.1 It is recommended that the primary steering position be located so that the person conning the vessel has a clear view for the safe navigation of the vessel, and be provided with a wheel or tiller positioned so as to permit full range of movement without obstruction.
11.2 The rudder should be so designed and positioned to maximize steering effectiveness under all conditions including angles of heel up to 60 degrees.
11.3 All steering gears, control cables, ropes or rods and pulleys or sheaves should be so positioned and guarded as to minimise the possibility of jamming by loose objects, at the same time providing access for inspection and lubrication.
11.4 Where means of power assistance for steering is provided, manual over-ride should be possible and an indication of failure of power should be provided at the helmsman's station.
11.5 All attachments and mountings of components of the steering gear should be of adequate strength, taking into consideration the loads associated with any power assistance or mechanical advantage.
11.6 In case of a failure resulting in loss of primary steering gear, an emergency means of steering should be available. Instructions for rigging and operating emergency steering gear should be posted adjacent to the helmsman's station.
11.7 The main steering system should be capable of putting the rudder over from 35 degrees on one side to 35 degrees on the other side with the ship at its deepest seagoing draught and running ahead at maximum service speed.
11.8 If the main steering system is power driven it should be capable of putting the rudder over from 35 degrees on either side to 30 degrees on the other side in not more than 28 seconds with the ship at its deepest seagoing draught and running ahead at maximum service speed.
11.9 The design pressure used in calculating scantlings of piping and other steering gear components subjected to internal hydraulic pressure should be at least 1.25 times the maximum working pressure to be expected under the operational conditions specified in paragraph 11.7 taking into account any pressure which may exists in the low-pressure side of the system. Fatigue analysis may be needed in the design of piping components, taking into account pulsating pressures due to dynamic loads if required by a TC inspector.
12. Fire Safety
12.1 General
12.1.1 To the maximum extent practical, all materials used in the hull construction, surface finishes, deck coverings and trim should be of low flame spread characteristic.
12.1.2 The deckhead immediately beneath survival craft stowages, and any adjacent bulkheads, should be insulated with a 30-minute rated fire insulation.
12.1.3 Any access which may be used as a means of escape to the weather deck should be constructed to B-15 standard as defined in the Hull Construction Regulations.
12.1.4 No material should be used in the construction, furnishing or decoration of accommodation spaces which emits excessive amounts toxic smoke and toxic gases when exposed to temperatures in excess of 60 °C .
12.1.5 Notwithstanding the provisions of 12.1.1, existing ships may retain any wood used in accommodation spaces.
12.1.6 Every ship should be equipped with at least one powered fire pump driven by a propulsion unit or independent source of power and should also be provided with a fire main, hydrants, hoses and nozzles.
12.1.7 There should be sufficient number of fire hydrants, each provided with one length of fire hose and located so that any part of the ship may be reached with an efficient stream of water.
12.1.8 Fire pumps may also be used as bilge pumps.
12.1.9 The fire main, water service pipes and fire hydrants should be constructed so that they will not corrode, will not be rendered ineffective by heat and be protected from freezing.
12.1.10 Every ship should have a portable fire pump located outside the machinery space and having a capacity of at least 1.1 m³/hr equipped with a suction and discharge hose suitable for use in fire fighting.
12.1.11 Any ducting carrying vapours or gases the temperature of which exceeds 60 °C . should be adequately insulated in way of any bulkhead or deck penetrations.
12.1.12 Any ducting carrying flammable or toxic vapours or gases should be constructed of incombustible material and should be securely supported and fastened.
12.1.13 To the maximum extent practical, electrical components and components containing flammable fluid should be separated by as great a distance as possible.
12.1.14 All fire detection and extinguishing equipment required by this standard should be of a type approved by a national recognised testing authority and should be in compliance with the Fire Detection and Extinguishing Equipment Regulations.
12.2 Living Spaces
12.2.1 Spaces used for messing and sleeping should be provided with smoke detectors and CO detectors with an audible alarm.
12.2.2 At least one Underwriters Laboratories of Canada ( ULC ) approved, 4.5 L foam extinguisher should be provided, secured in a prominently identified stowage, in each compartment used for messing.
12.2.3 In each space containing sleeping berths, at least one, 1 kg dry chemical extinguisher should be provided.
12.2.4 At least one, 4.5 L foam or 1 kg dry chemical extinguisher should be provided immediately adjacent to any cooking appliance.
12.2.5 Where messing, sleeping and/or galley spaces are contiguous, the requirements for fire extinguishers contained in para. 12.2.2 - 12.2.4 should be complied with as if the spaces were separate. Equivalent fire appliances should be considered on their own merit. Where mess areas are adjacent to machinery spaces, divisions between the spaces are to be gas tight.
12.3 Fire Hazard Areas
12.3.1 Spaces used for storage of flammable materials such as paint or oil should be provided with a certified safe type smoke detector giving an audible alarm; the detector should be certified for use in the dangerous environment to which it may be exposed.
12.3.2 A minimum of one 9 L foam or equivalent A, B or C type multi-purpose extinguisher should be provided for every 15 m in length, immediately adjacent to the entrance of any space in which flammable materials are stored, secured in a prominent stowage (see following Table for extinguishers equivalencies).
12.3.3 The interior surfaces of the boundaries of spaces in which flammable materials are stored should be constructed to B-15 standard.
12.3.4 The exposed surfaces surrounding installed cooking and/or heating appliances should be of, or protected by, incombustible material.
12.3.5 At least one 4.5 kg dry chemical fire extinguisher or equivalent should be provided for each pantry / galley having cooking facilities.
12.3.6 Provision should be made to positively exhaust cooking vapours to the atmosphere; means should be provided to permit the removal of any accumulation of oil or grease from the exhaust duct. The ventilation trunking should be provided with a means of weathertight closure. The trunking should be incombustible and should be insulated in way of any structural penetrations.
Table 1: Equivalents for Fire Extinguishers
| Type | Water ( L ) | Foam ( L ) | Carbon Dioxide ( kg ) | Dry Chemical ( kg ) |
|---|---|---|---|---|
| A | 9 | 9 | 2 multi-purpose |
|
| B | 9 | 7 | 4.5 | |
| B | 46 | 16 | 9 | |
| B | 76 | 23 | 14 | |
| B | 151 | 45 | 23 | |
| C | 2 | 1 | ||
| C | 7 | 4.5 |
12.4 Machinery spaces
12.4.1 Any space containing machinery should be provided with a fire detection device giving an audible alarm which can be heard outside of the machinery spaces as well a visual signal; the detector should be re-settable, and should include a test facility.
12.4.2 Any space containing machinery should be provided with a fixed fire extinguishing system, which may consist of a portable extinguisher, with two charges each capable of total flooding of the space with carbon dioxide or TC approved equivalent fire extinguishing medium. Means should be provided to close openings which would admit air into such spaces.
12.4.3 Fixed fire extinguishant discharge should be from one remote control, which should be provided with a positive guard, clearly labelled, in a control point position.
12.4.4 Fixed fire extinguishant should be stored in securely fastened containers with a positive identification outside the space being protected; containers should be provided with a positive indication of their contents except in the case of CO2 systems where pressure does not permit such indication. All systems should be recertified annually.
12.4.5 Notwithstanding 12.4.3, if the primary means of activating discharge of extinguishant is electrical, a manual means of activation should also be provided.
12.4.6 When the ship is constructed of wood, the exposed surfaces within the engine space should be treated with an approved flame retardant coating of intumescent paint or equivalent.
12.4.6 When the ship is constructed of fibreglass reinforced plastic ( FRP ) flame retardant additives should be incorporated in the exposed layer of resin within the engine space or the final layer of hull lay-up should be of woven rovings. When either of these has not been done, the application of an intumescent paint may be accepted as providing equivalent protection
12.4.8 Any boundaries of machinery spaces which are adjacent to accommodation spaces or escape routes should be insulated to at least B-15 standard and such spaces in new sail training ships should be gas-tight.
12.4.9 Any electrical equipment installed in a machinery space should be of a type so enclosed and protected as to prevent the escape of sparks.
12.4.10 Penetrations of boundaries of machinery spaces should not impair the fire safety of such boundaries.
12.5 Fuel Systems and Stowages
12.5.1 Fuel oil used in fixed installations, should have a flash-point of no less than 60 °C (closed cup test). It is recommended that oil fuel tanks be located outside of machinery spaces and be constructed of steel.
12.5.2 Each fuel line penetrating a machinery space boundary should be provided with a remote control shut-off valve fitted on the tank or, where impractical, with a clearly identified rapid acting shut-off valve immediately outside the machinery space, ensuring ready access to such valves at all times.
12.5.3 Any gasoline required to be carried as fuel for survival craft engines should be kept to the absolute minimum and should be securely stowed on the weather deck, clear from any normal work area, and appropriately placarded.
12.5.4 Gasoline stowages should be of brass, bronze, plastic or other material which will not generate sparks and which is impervious to gasoline.
12.5.5 Any tanks used for the stowage of gasoline should be to a standard approved by C.S.A.
12.5.6 Portable fuel tanks should be secured so that when full, they will be retained at angles of heel up to 60 degrees and under loads associated with 2 g acceleration.
13. Life Saving and Emergency Equipment
13.1.1 Every ship should carry survival craft which may include either emergency boats, liferafts, inflatable or rigid, or a combination thereof.
13.1.2 Survival craft should be provided in such numbers and capacity to accommodate at least the total number of persons on board. In addition, in the event of any one liferaft being lost or rendered unserviceable, there should be sufficient survival crafts to accommodate the total number of persons on board.
13.1.3 The means of securing survival craft should be of sufficient strength to withstand acceleration forces of up to 2 g in any direction with the ship heeling up to 60 degrees.
13.1.4 Survival craft should be capable of rapid release from their stowages without the need for special tools; where necessary, means of operating release mechanisms should be clearly described at the stowage. These instructions should be in pictographic form.
13.1.5 Each survival craft should be equipped with a painter of adequate strength and length to hold the craft secured alongside with the ship heeled up to 60 degrees. This painter should be secured to the ship at all times.
13.1.6 Inflatable liferafts should be carried in approved containers, and should be equipped with hydrostatic release units and stowed in such a manner as to allow the container to float free without hindrance from vessel’s structure, rigging or other items of equipment.
13.1.7 Boats should be stowed completely equipped, rudder and tiller shipped, and with oars, rowlocks or loose equipment securely stowed. Where so equipped, boat engines, fuel tanks and batteries should be maintained in the boat ready for use in case of emergency.
13.1.8 All boats should be marked permanently with the ship's name and port of registry with characters not less than 75 mm high, in a colour contrasting to the background.
13.1.9 Spare fuel tanks for survival craft engines should be securely stowed in a clearly identified stowage on the weather deck; if the stowage is enclosed, it should be provided with a vent whose discharge is remote from any normal working station and which is fitted with a protective flash screen. All boats should have affixed retro-reflective tape in accordance with requirements of the Canadian General Standards Board.
13.1.10 The spare fuel tank stowage should be provided with means of containing any fuel leakage.
13.2 Lifejackets
13.2.1 Every ship should carry Transport Canada approved lifejackets sufficient for 125% of the persons on board.
13.2.2 Lifejackets should be securely stowed in readily accessible and clearly identified stowages. Lifejackets should be marked with the ship’s name and port of registry.
13.2.3 Lifejacket stowages should afford maximum protection against mechanical damage and atmospheric deterioration of the lifejackets, and should be remote from any potentially hazardous location.
13.3 Other Life Saving Equipment
13.3.1 Every ship should carry a minimum of 3 Transport Canada approved lifebuoys.
13.3.2 At least one lifebuoy on each side is to be equipped with:
- a whistle;
- a self-igniting light and self-activating smoke signal; or
- a self-igniting light that is visible by day or night;
and at least one other lifebuoy on each side is to be equipped with a buoyant line of not less than 30 m in length.
13.3.3 All lifebuoys should be arranged so that they may be released clear of the side of the ship by a quick-release device and should be located in readily accessible stowages close to the side of the ship, spaced approximately equidistantly along the length of the weather deck in the normal working area.
13.3.4 Every ship should carry a man overboard ( MOB ) pole.
13.3.5 Every ship should carry an efficient fixed or portable searchlight suitable for use in MOB search and recovery operations.
13.3.6 Every ship should carry a boarding ladder, scrambling net to at least 600 mm below the waterline or some other means of permitting the retrieval of persons from the water and a life sling rigged to pick up from the water a body of at least 100 kg .
13.3.7 Every ship should carry a minimum of 6 distress flares of type A or type B or type C and a minimum of 6 distress signals of either type A, B or C or type D, carried in a weathertight buoyant stowage on the weather deck.
13.4 Emergency Equipment
13.4.1 Every ship should carry at least one approved first-aid kit.
13.4.2 Every ship should be fitted with an eye wash station conveniently located adjacent to the battery maintenance area.
13.4.3 Every ship should carry a sail repair kit containing sail material, thread, sailmaker's palms, needles, cringles, fids and marline spikes as appropriate to the sails carried.
13.4.4 Every ship should carry such tools and material relevant to the material of hull construction which may be required to cover or patch damage or leaks.
13.4.5 Every ship should carry means of effecting repairs to the steering system, including an emergency tiller or equivalent.
13.4.6 Every ship should carry wire cutting equipment for use in the event of dismasting.
14. Communication Equipment
14.1 Radiocommunication
14.1.1 Every ship should comply as appropriate with the Ship Station Radio Regulations ( SSRR ), as amended and, the Ship Station Technical Regulations ( SSTR ), as amended, and with the following provisions of this standard which exceed or complement these regulations.
14.1.2 Every ship should carry at least one VHF radiotelephone capable of transmitting and receiving on 156.8 MHz and marine communication frequencies appropriate to the area of operation. The ship should therefore comply with the VHF Practices and Procedures Regulations.
14.1.3 Any ship intending to operate beyond the coverage area of a VHF coast station should carry at least one MF radiotelephone capable of transmitting and receiving on 2182 KHz , and capable of two-way communication with ship and shore stations within MF range.
14.1.4 Every ship should carry at least one portable VHF two-way radiotelephone for use in the event of having to abandon ship. Portable VHF radiotelephones intended for this purpose should be securely stowed and readily accessible at the position from which the ship is normally navigated. The portable radiotelephone should be waterproof (or sealed in a waterproof container). Each portable radiotelephone should have a dedicated primary battery for use only in an emergency (with breakable seal to indicate that it has not previously been used). The portable radiotelephone should be capable of operating on VHF channel 16 and at least one additional channel.
14.1.5 Ships intending to navigate beyond Home Trade IV or Minor Waters as defined in the Home-Trade, Inland and Minor Water Voyages Regulations for periods in excess of 24 hours should carry at least one 406 type emergency position-indicating radio beacon ( EPIRB ) stowed in such a manner that it will be protected from damage ready for immediate use and for placing into the survival craft, but will float free in the event of the ship sinking. The EPIRB should meet the requirements of the SSTR section 58.01.
14.1.6 Radiotelephone antennae should be equipped with a means of grounding for use in electric storms, or should be protected by lightning arrestors or protective gaps.
14.2 Visual Signals
14.2.1 Ships should carry one daylight signalling lamp, capable of operating independently of the ship's main electrical system. The lantern should normally be stowed in the main navigation position.
14.2.2 Every ship should carry one set of flags of the International Code of a size suitable for signalling.
15. Navigation Equipment
15.1 General
15.1.1 Every ship should comply as appropriate with the Navigating Appliances and Equipment Regulations and the Charts and Publications Regulations. In addition to the provisions of the preceding regulations, all ships should comply with the provisions of this Standard that exceed such regulations.
15.1.2 Every ship should be equipped with a compass, capable of being corrected, and located in a position such that the compass card is readily visible by the helmsman at the primary steering position. The compass should be fitted with a pelorus or if not, a separate hand bearing compass should be provided.
15.1.3 Every ship should be equipped with an electronic means of measuring water depth continuously; in addition, a hand lead line, provided with traditional markings, of not less than 20 fathom length and with a lead, capable of being armed, of not less than 3.2 Kg , should be provided.
15.1.4 Every ship should carry the latest editions, corrected up to date of the following publications appropriate to the operating area:
- Charts
- Tide and Current Tables
- List of Lights, Buoys and Fog Signals
- Sailing Directions
- Notices to Mariners
- Radio Aids to Marine Navigation
- International Code of Signals
- Code of Nautical Practices
- Watchkeeping Standards
15.1.5 Any ship intending to navigate out of sight of land for more than 24 hours should carry a sextant and a chronometre or efficient time piece and, in addition to the publications quoted in 15.1.4, nautical almanacs and tables.
15.1.6 All magnetic compasses and any sextants, chronometres and time pieces carried, should be provided with appropriate correction data.
15.1.7 Due provision should be made to prevent damage or the risk of fire in the event of lightning striking antennae or conductors of any navigation equipment.
15.1.8 Every ship should carry a minimum of one GPS and a radar system.
15.1.9 Every ship should carry a log book.
15.2 Lights, Shapes and Sound Signals
15.2.1 Every ship should comply with the Collision Regulations and with the following provision of this Standard which exceed or complement these regulations.
15.2.2 Every ship should be able to exhibit lights and day shapes as required by the Collision Regulations, including:
- 2 all-round red lights near the top of the tallest mast,
- 1 all-round white light in the fore-triangle.
By day, the lights required by a) and b) should be replaced by 2 black balls and 1 black ball, respectively.
15.2.3 The lights required by the Collision Regulations should be electrically powered; in addition, a duplicate set of sidelights, stern light and masthead lights, if applicable, with an alternative source of power should be provided together with secure means of mounting.
16. Anchors and Cables
16.1 Every ship should be provided with at least two high holding power ( HHP ) anchors and cables in accordance with the following table of minimum sizes. The anchor sizes given in the table are for HHP types i.e. spade, plough, etc.
16.2 The requirements shown in the table below are for ships of normal sailing yacht form. Where such ships have an unusually high windage, such as heavy rigging, viz. square-rigger, or large superstructures, the weight of each anchor should be increased by 25%. The diametre of the anchor cable should be appropriate to the weight of the increased size of anchor.
16.3 If a fisherman type of anchor is to be provided, the weight from the table should be increased by 75% but the diametre of the anchor cable need not be increased.
16.4 The length of each anchor cable should be appropriate to the operating area but in any event should not be less than 55 m for both the main and kedge anchors. The anchor cable for the main anchor should be of chain or equivalent and for the kedge anchor may be of rope. Where the anchor cable is of rope, there should be at least 5 m of chain between the rope and the anchor. At least one anchor should be provided with a permanently secured rode, the outboard end of which should terminate in chain, and the bitter end should be permanently secured to the ship.
16.5 The ship should be provided with a towline of not less than the length and diametre of the kedge anchor cable. The towline may be used as a warp for the kedge anchor.
16.6 Where an anchor weighs more than 50 kg , an adequate windlass should be provided for working the anchor.
16.7 There should be a strong securing point on the foredeck and a fairlead or roller at the bow which can be closed over the cable.
16.8 Provision should be made to securely fasten each anchor when stowed or catted.
16.9 Every ship should have a means of emergency anchoring with no power available.
Table 2: Anchors and Cables
| Length Overall | Anchor Weight | Anchor Cable Diameter | ||||
|---|---|---|---|---|---|---|
| Main | Kedge | Main | Kedge | |||
| Chain | Rope | Chain | Rope | |||
| (metres) | ( kg ) | ( kg ) | ( mm ) | ( mm ) | ( mm ) | ( mm ) |
| Up to 9 | 15 | 8 | 8 | 12 | 6 | 10 |
| 10 | 17 | 9 | 8 | 14 | 8 | 12 |
| 11 | 20 | 10 | 8 | 14 | 8 | 12 |
| 12 | 23 | 12 | 8 | 14 | 8 | 12 |
| 13 | 26 | 13 | 9.5 | 16 | 8 | 12 |
| 14 | 30 | 15 | 9.5 | 16 | 8 | 14 |
| 15 | 34 | 17 | 9.5 | -- | 8 | 14 |
| 16 | 38 | 19 | 11 | -- | 8 | 14 |
| 17 | 44 | 22 | 11 | -- | 8 | 14 |
| 18 | 50 | 25 | 11 | -- | 9.5 | 16 |
| 19 | 56 | 28 | 12.5 | -- | 9.5 | 16 |
| 20 | 62 | 31 | 12.5 | -- | 9.5 | 16 |
| 21 | 69 | 35 | 12.5 | -- | 11 | 16 |
| 22 | 76 | 38 | 12.5 | -- | 11 | 16 |
| 23 | 83 | 42 | 14 | -- | 11 | 16 |
| 24 | 90 | 45 | 14 | -- | 11 | 16 |
Notes:
- Chain cable diametre given is for short link. Where stud link cable is to be used, the diametre may be modified in accordance with the breaking load.
- The rope diametre given is for nylon. Where other fibres are to be used, the diametre should be modified in accordance with the breaking load.
- Where a heavier kedge anchor is provided, the weight of the main anchor may be reduced provided the combined weight of both anchors is not less than 160% of the main anchor weight.
17. Miscellaneous Marine Equipment
17.1 Every ship should be provided with a minimum of two bollards with adjacent fairleads for each side of the weather deck.
17.2 Every ship should be provided with an adequate deck fitting suitable for accepting a hawser for towing the ship.
17.3 An inclinometer should be fitted on the ship's centre line, in or adjacent to the steering position, control point or chartroom.
17.4 Every ship should be equipped with an anemometer, which may be fixed or portable.
17.5 Every ship should be equipped with a barometer.
17.6 Every ship should carry binoculars.
18. Accommodation
18.1 Living Spaces
18.1.1 In every ship intended to sail on overnight voyages, each person on board should be provided with a bunk and an easily accessible stowage area for stowing dry clothing and personal effects.
18.1.2 Bunks may be in tiers, provided that berths have a minimum vertical space of 600 mm . It is recommended that overlap does not exceed 60% for bunks having small vertical spacing.
18.1.3 Each bunk should be designed to accept a leeboard or leecloth.
18.1.4 Each bunk should be immediately adjacent to a gangway or passageway leading to an escape route.
18.1.5 Hammocks may be substituted for bunks, provided that they do not significantly obstruct movement; appropriate stowages for hammocks should be provided.
18.1.6 Every living space below the weather deck should be provided with at least two escape routes, at least one of which should be directly to the weather deck.
18.1.7 It is recommended that routes leading to the weather deck from living spaces be located as far as practical from a potential fire source, and as close as possible to the longitudinal centreline.
18.1.8 No space should be used as living space forward of 5% of the waterline length, measured aft from the stem at the waterline.
18.1.9 Adequate provision should be made for hanging and stowing wet clothing, so far as practical in spaces not normally designated as living space.
18.1.10 Living spaces should be adequately lighted and ventilated; all openings which may be used for natural ventilation should be provided with effective means of closure; openings in weather deck should be capable of weathertight closure; side scuttles should be capable of watertight closure.
18.1.11 Adequate containers for garbage should be provided in living spaces.
18.2 Toilets and Washplaces
18.2.1 A minimum of one toilet space should be provided for every 15 persons on board; toilet spaces should be totally enclosed and should be provided with ventilation providing not less than 10 air volume changes per hour.
18.2.2 All toilets should be of an approved marine type; where sea water is used for flushing, the sea water inlet should be immediately adjacent to the toilet and provided with a shut-off cock or valve at the through-hull fitting.
18.2.3 At least one hand-basin should be provided for every 15 persons on board; any sea-water inlets should be by way of a shut-off cock or valve at the through-hull fitting adjacent to the hand-basin.
18.2.4 All sewage and grey water should be effectively drained to respective holding tanks (see Section 8) if required by law.
18.3 Galleys
18.3.1 Every ship intended to sail on overnight voyages should be equipped with a galley containing cooking facilities, food storage facilities with temperature control commensurate with food to be stored, appropriate food preparation area, and wash-up area.
18.3.2 Cooking, refrigeration and heating appliances may use any fuel except gasoline, or be electrically powered. Liquid or gaseous fuel should either be provided from a remote bulk storage, or should be limited to quantities not exceeding 2 l (liquid) or 500 grams (gaseous) fuel directly connected.
18.3.3 Bulk storage of cooking fuel should be supplied to the galley area by appropriate piping securely fastened, and routed to the maximum practical extent clear of other accommodation spaces. Pipe penetrations of any bulkheads or decks should be through protective glands to minimise any chafing. Piping and appliances to be used with Liquefied Petroleum Gas ( LPG ) or Compressed Natural Gas ( CNG ) for cooking purposes should meet at least the National Fire Protection Association ( NFPA ) or American Boat & Yacht Council ( ABYC ) standards.
18.3.4 Cooking stoves may be arranged in gimbals or fiddles which can be locked when the ship is alongside, and fuel connections should be arranged to compensate for relative movement. Stoves should provide adequate protection against spillage by use of fiddles.
18.3.5 Where gaseous fuel is used, the galley area should be protected by an appropriate vapour detector, appropriately located, which provides an audible alarm and activates a supply shut-off valve at the storage point.
18.3.6 Gaseous fuel should be contained in approved containers in a space directly open to atmosphere and adequately secured against loads associated with 2 g at angles of heel up to 60 degrees. Where multiple containers are used, they should be connected to a common supply line through isolating valves immediately downstream of the containers.
18.3.7 The installation of the gaseous fuel systems should be carried out by a Canadian Gas Association certificated technician.
18.3.8 All food storage and cooking facilities should be adequately secured, and provide for retention of food or containers, to withstand loads associated with 2 g at angles of heel up to 60 degrees.
18.3.9 The galley should be ventilated, and the ventilation trunking should be provided with a means of weathertight closure. The trunking should be incombustible, and should be insulated in way of any structural penetrations.
18.3.10 Every galley should be provided with adequate number, size and type of fire extinguishers, but in no case less than one 4.5 litre fire extinguisher of appropriate type.
19. Protection of Personnel
19.1 General
19.1.1 The surface of the working deck should be non-slip. Acceptable surfaces are: unpainted wood; a non-slip pattern moulded into FRP ; non-slip deck paint; or an efficient non-slip covering. Particular attention should be paid to hatch covers where these are fitted on the working deck and to sloping coachroof sides where these effectively constitute a working deck when the ship is heeled.
19.1.2 A toe rail of not less than 25 mm in height should be fitted around the working deck.
19.2 Bulwarks and Guard Rails
19.2.1 The perimetres of weather decks should be fitted with bulwarks, guard rails or guard rope of sufficient strength and height.
19.2.2 In general, taut double guard rails with the upper rail or rope at a height of not less than 600 mm above the deck should be fitted around the perimetre of the weather deck. They should be supported at intervals not exceeding 2.2 m.
19.2.4 If the cockpit opens aft to the sea, additional guard rails should be fitted so that there is no vertical opening greater than 500 mm .
19.2.5 There should be a fixed bow pulpit forward of the forestay of at least the same height as the guard rails except in way of a substantial bowsprit for which an appropriate netting should be provided.
19.2.6 There should be sufficient hand holds and grab rails within the accommodations including access stairways and ladderways to allow safe movement throughout accommodation spaces at all times.
19.3 Safety Harnesses
19.3.1 One safety harness, which may be rapidly attached to, and detached from the lifelines should be provided for each person on board.
19.3.2 Dedicated lines should be provided, stowed securely on the weather deck, for use as lifelines in heavy weather, of sufficient length to extend fore and aft along the deck on each side along the normal working area.
19.3.3 Provisions should be made on the weather deck to adequately secure the lifelines to provide maximum assistance to crew movement with minimum obstruction to hatches, survival craft or handling running rigging.
19.3.4 Fastening points for the attachment of safety harness should be provided in the following positions;
- close to the companionway; and
- on both sides of the control station.
19.3.5 Efficient means of securing the lifelines of safety harnesses should be provided on exposed decks.
19.3.6 Every ship should be fitted with grab rails on the sides and ends of deck houses.
19.4 Fall Arrest Systems
19.4.1 Every person who works aloft should wear an approved full body fall arrest harness and be trained in its use.
19.4.2 The D-ring attachment point should not be below the person’s centre of gravity.
19.4.3 Lanyards attached to harnesses for working aloft should not be longer than three feet, or equivalent metric length, unless equipped with a shock absorber.
19.4.4 Lanyards and carabiners should be CSA approved, equivalent to or exceeding their safety specifications.
19.4.5 Chest harnesses are acceptable for work on deck.
19.4.6 Every mast and spar upon which crew members may be required to work in the normal course of sailing should be provided with attachment points for fall arresting devices.
19.4.7 One fall arresting device should be provided for each crew member required to work more than 2 m above the weather deck.
19.4.8 Yard jackstays and hardware employed should be capable of handling all associated loads.
19.4.9 Attachment points should be provided to enable individuals to traverse safely the futtock shrouds while attached.
19.5 Safety Procedures
The master of a sail training ship carrying trainees should ensure that each trainee:
- as soon as practical after joining the ship for the first time is given instruction designed to make him familiar with the layout of the ship; and
- as soon as practical after joining the ship and at intervals thereafter not exceeding one week is given training in safety procedures, including the use of fire fighting and life saving appliances of the ship.
Appendix A: Sample Stability Information Booklet
A 1 General Particulars
- Ship's name
- Official NumberFootnote 1
- Port of RegistryFootnote 1
- Owner's Name and Address
- ClassFootnote 2
- Builder
- Date Construction Started
- Dimensions
Length overall including bowsprit
metres
Length
metres
Length on waterline
metres
Maximum beam
metres
Depth Footnote 3
metres
Displacement fully laden
tonnes
Draught fully laden Footnote 4
metres
Minimum freeboard
metres
Gross tonnage
A 2 Arrangement of Sections
This booklet is arranged in sections so that the most essential matters are brought to the user's attention first.
Section 1- Operational Information This section contains guidance intended to ensure that the level of stability may be judged with reference to a recomrnended maximum steady angle of heel to prevent downflooding in gusts and squalls.
Section 2 - Technical Data and Loading Conditions This section details the loading conditions upon which the recommended heeling angles are based.
Section 3 - Reference Information This section contains basic information which is necessary for the calculations in Sections 1 and 2. It is not necessary for the skipper to refer to this part but the Beaufort scale and the metric/imperial conversion table may be useful.
Section 1: Operational Information
A 3.1 Arrangement of Tanks and Ballast
Figure 4: Tank and Ballast Arrangement
- Fuel tank (port)
- Fuel tank (starboard)
- Fresh water tank
- Fresh water tank
- Sewage tank
- Lead ballast keel (18 tonnes)Footnote 1
- Draughts are referred to an extension of the underside of keelFootnote 2
- All other vertical locations are referred to BASEFootnote 3
- All longitudinal locations are referred to MIDSHIPS
- Trim is defined as: Draught Aft - Draught Fwd
- Design trim = Rake of keel = 1.10 metres
A 3.2 Sail Plan
| Sail | Area m² |
Height of Centroid Above Base m |
|---|---|---|
| 1. No. 1 lib | 125 | 13.2 |
| 2. No. 2 lib | 70 | 11 |
| 3. Staysail | 45 | 10. |
| 4. Mainsail | 100 | 13.1 |
| 5. Mizzen | 40 | 10.3 |
| 6. Storm Jib | 27 | 8.2 |
| 7. Trisail | 28 | 9.61 |
Figure 5: Sail Plan
A 3.3 Angles of Deck Edge Immersion and Downflooding
| Description | Area of Opening m² | Angles of Immersion | |
|---|---|---|---|
| 100% Consumables degrees | 10% Consumables degrees | ||
| Deck Edge | -- | 24 | 27 |
| Main companionway | 0.80 | 84 | 89 |
| Fwd companionway | 0.65 | 92 | 97 |
| Aft skylight | 0.11 | 63 | 70 |
| Fwd skylight | 0.11 | 52 | 57 |
| Galley VentFootnote 4 | 0.11 | 45 | 47 |
Critical downflooding is deemed to occur when the lower edges of openings having an aggregate area (in m² ) greater than
(displacement (in tonnes) / 1500) are immersed
i.e. 65/1500 = 0.04 m²
Thus immersion of the galley vent is not regarded as critical and it is the irnmersion of the forward skylight which defines the critical downflooding angle referred to in this booklet.
The master should note that the presence of the vent and skylights significantly reduce the ability of this vessel to withstand downflooding and with these openings securely closed the safety of the vessel is enhanced considerably.
A 3.4 Notes on Stability for the Guidance of the Master
- Compliance with the stability criteria indicated in the booklet does not ensure immunity against capsizing regardless of the circumstances or absolve the master from his responsibilities. Masters should therefore exercise prudence and good seamanship having regard to the season of the year, experience of the crew, weather forecasts and navigational zone, and should take appropriate action as to the speed, course and sail setting warranted by the prevailing conditions.
- Before a voyage comrnences, care should be taken to ensure that sizeable items of equipment have been properly stowed to minimize the possibility of both longitudinal and transverse shifting under the effect of accelerations caused by pitching and rolling, or in the event of a knockdown to 90 degrees.
- In adverse weather conditions and when there is the possibility of encountering a severe gust, squall or large breaking wave, all exposed doors, hatches, skylights, vents, etc. should be closed and securely fastened to prevent ingress of water. Storm boards etc. should be erected and fitted.
- The amount of sail carried is at the discretion of the Master and his decision will have to take into account many factors. In assessing the risks of downflooding, the Master should be guided by Figures 6 and 7.
- Figure 6 shows the maximum recommended steady heel angle to prevent downflooding in gusts. Operation of the vessel at a greater heel angle would result in downflooding if it were to encounter the strongest possible gust in the prevailing turbulent airstream, which could exert a heeling moment equal to twice that of the mean wind.
- Figure 7 shows the maximum recommended steady heel angle to prevent downflooding in squalls. Operation of the vessel at a greater heel angle would result in downflooding if it were to encounter the heeling effects of a squall arising from a storm cell or frontal system which may result in a heeling moment many times greater than that of the mean wind. For this reason the master should have regard to the maximum steady heel angle curves presented for a range of squall speeds.
- By using the readings from his inclinometer and anemometer a Master is able to detemmine the degree of risk of capsize in gusts or squalls which may occur in the prevailing weather system. He may then decide to shorten sail together with other actions he considers necessary.
- Additional care should be taken when sailing with the wind from astem as, in the event of the vessel broaching or a gust striking the vessel on the beam, the heeling effects of the wind may be increased to a dangerous level when the preceding heel angle was small.
A 3.5 Maximum Steady Heel Angle to Prevent Downflooding in Gusts.
Figure 6: Maximum Heel Angle, Gusts
Gusting Conditions
When sailing in a steady wind the vessel heels to the angle at which the heeling arm curve intersects to GZ curve. When struck by a gust the heel angle will increase to the intersection of the gust heeling arm curve with the GZ curve. The heeling moment increases in proportion to the square of the apparent wind speed.
Operation of the vessel at a mean heel angle not greater than 27 degrees ensures significant downflooding openings would not be immersed if it were to encounter the strongest gust in the prevailing turbulent airstream which could exert a heeling moment equal to twice that of the mean wind ( i.e. mean apparent wind has increased in velocity by 1.4).
A 3.6 Curves of Maximum Steady Heel Angle to Prevent Downflooding in Squalls
Figure 7: Maximum Steady Heel Ange, Squalls
Squall Conditions
Curves of maximum steady heel angle indicate the range of mean or steady heel angles beyond which the vessel will suffer downflooding in the event of a squall.
Operation of the vessel in cyclonic conditions particularly in the hours of darkness, where severe squalls are imminent requires the recommended maximum steady heel angle to be reduced depending on the mean apparent wind speed in accordance with the curves presented above.
A 3.7 Examples Showing the use of the Maximum Steady Heel Angle Curves
Figure 8: Maximum Steady Heel Angle Curves
Example A
The yacht is reaching, with a steady apparent wind speed of 16 knots. The mean heel angle is 15 degrees. Forecasts and visible cumulo-nimbus clouds suggest squalls may be imminent. By plotting the heel angle and wind speed (point A in Figure 8) the indication is that the vessel will be in danger of heeling to the downflooding angle in squalls in 30 knots. In order to increase safety from downflooding, say, to withstand squalls of up to 45 knots, sails should be handed or reefed to reduce the mean heel angle to 7 degrees (point A1 in Figure 3) or less.
Example B
The yacht is beating in gusty conditions with a mean apparent wind speed of 30 knots. The mean heel angle is 20 degrees. No squalls are expected. The heel angle is significantly less than 27 degrees, the maximum recommended steady heel angle, and there is therefore a good safety margin against downflooding in a strong gust. Plotting these values of wind speed and heel angle (point B in Figure 8) also indicates that the vessel would not be vulnerable to downflooding in a squall unless it resulted in a wind speed in excess of about 50 knots. There is thus no need to reduce sail area on the ground of stability.
Note: Appropriate examples should be presented for the Master, to enable him to interpret the meaning of these curves and understand their use.
Section 2: Technical Data and Loading Conditions
A 4.1 Freeboard Marks
Figure 9: Freeboard Markings
A 4.2 Tank Capacities
| Tank | Capacity m³ |
Weight tonnes |
LCG mfWd base |
VCG Mabove |
FSM tonne.m |
|---|---|---|---|---|---|
| FuelP 1.06 | 0.92 | -2.4 | 2.03 | 0.13 | |
| FuelS 1.06 | 0.92 | -2.4 | 2.03 | 0.13 | |
| FW Aft | 0.70 | 0.70 | -7.0 | 2.30 | 0.10 |
| FW Fwd | 1.12 | 1.12 | -0.2 | 1.03 | 0.56 |
| Sewage | 0.80 | 0.80 | 2.1 | 1.11 | 0.24 |
A 4.3 Loading Conditions and GZ Curves
Condition 1: Fully Laden Departure
Table 4: Weights and Displacement, Fully Laden
| Item name | Weight tonnes |
LCG Metres |
LMOM Tonne M |
VCG Metres |
VMOM Tonne M |
FSM Tonne M |
|---|---|---|---|---|---|---|
| Fuel (Port) | 0.92 | -2.400 | -2.21 | 2.030 | 1.87 | 0.1 |
| Fuel ( Starboard ) | 0.92 | -2.400 | -2.21 | 2.030 | 1.87 | 0.1 |
| Fresh Water (Aft) | 0.70 | -7.000 | -4.90 | 2.300 | 1.61 | 0.1 |
| Fresh Water ( Fwd ) | 1.12 | -0.200 | -0.22 | 1.030 | 1.15 | 0.6 |
| Sewage Tank | 0.08 | 2.100 | 0.17 | 0.700 | 0.06 | 0.0 |
| Stores | 1.00 | 0.000 | 0.00 | 2.500 | 2.50 | 0.0 |
| Crew & Effects | 1.80 | 0.000 | 0.00 | 3.600 | 6.48 | 0.0 |
| Margin for Growth | 2.80 | 0.000 | 0.00 | 3.880 | 10.86 | 0.0 |
| Deadweight | 9.34 | -1.003 | -9.37 | 2.826 | 26.40 | 0.9 |
| Lightship | 56.04 | -0.311 | -17.43 | 2.234 | 125.19 | 0.0 |
| Displacement | 65.38 | -0.410 | -26.80 | 2.319 | 151.59 | 0.9 |
- Draught Aft: 3.339 Metres
- Draught Forward: 2.094 Metres
- Mean Draught: 2.717 Metres
- Trim: 1.246 Metres by the stern
- GM Solid: 1.424 Metres
- GM Fluid: 1.410 Metres
Figure 10: Stability Curve: Fully Laden
Condition 2: Arrival with 10 Consumables
Table 5: Weights and Displacement, Arrival with 10 Consumables
| Item name | Weight Tonnes |
LCG Tonnes |
LMOM Tonne M |
VCG Tonnes |
VMOM Tonne M |
FSM Tonne M |
|---|---|---|---|---|---|---|
| Fuel (port) | 0.09 | -2.400 | -0.22 | 1.500 | 0.14 | 0.0 |
| Fuel ( Starboard ) | 0.09 | -2.400 | -0.22 | 1.500 | 0.14 | 0.0 |
| Fresh Water (aft) | 0.07 | -7.000 | -0.49 | 1.900 | 0.13 | 0.0 |
| Fresh Water ( Fwd ) | 0.11 | -0.200 | -0.02 | 0.700 | 0.08 | 0.0 |
| Sewage Tank | 0.70 | 2.100 | 1.47 | 1.000 | 0.70 | 0.2 |
| Stores | 0.10 | 0.000 | 0.00 | 2.500 | 0.25 | 0.0 |
| Crew & Effects | 1.80 | 0.000 | 0.00 | 3.600 | 6.48 | 0.0 |
| Margin for Growth | 2.80 | 0.000 | 0.00 | 3.880 | 10.86 | 0.0 |
| Deadweight | 5.76 | 0.091 | 0.53 | 3.259 | 18.77 | 0.2 |
| Lightship | 56.04 | -0.311 | -17.43 | 2.234 | 125.19 | 0.0 |
| Displacement | 61.80 | -0.274 | -16.90 | 2.330 | 143.27 | 0.2 |
- Draught Aft: 3.208 Metres
- Draught Forward: 2.121 Metres
- Mean Draught: 2.664 Metres
- Trim: 1.087 Metres by the stern
- GM Solid: 1.395 Metres
- GM Fluid: 1.391 Metres
Stability Curve for Condition 2
Figure 11: Stablility Curve, Arrival with 10% Consumables
Section 3: Reference Information
A 5.1 Notes on the Use of Free Surface Moments
Provided a tank is completely filled with liquid no movement of the liquid is possible and the effect on the ship's stability is precisely the same as if the tank contained solid material.
Immediately a quantity of liquid is withdrawn from the tank the situation changes completely and the stability of the ship is adversely affected by what is known as the "free surface effects". This adverse effect on the stability is referred to as a "loss in GM " or as a "virtual rise in VCG " and is calculated as follows:
Loss in GM due to Free Surface Effects:
Free Surface Interia (m4) x Density of Liquid in Tank (Tonnes/m³) / Displacement of Vessel (Tonnes)
= Free Surface Moment (Tonne.m) / Displacement of Vessel (Tonnes)
The free surface moments listed in the Tank Capacities Table refer to isolated tanks. If tanks are cross coupled the free surface moments will be considerably greater. Cross connection valves should therefore remain closed when the vessel is at sea.
A 5.2 Hydrostatic Plot
Figure 12 - Hydrostatic Curves
A 5.3 Cross Curve Plot
Figure 13 - Cross Curves
A 5.4 Notes on the use of KN Cross Curves
KN curves for displacements of 25 to 75 tonnes are presented for angles of heel at intervals between 10 and 140 degrees. The hull, main deck and enclosed deckhouses (see Figure 4 below) are assurned watertight at all angles of heel1.
To obtain righting arm ( GZ ) curves at a given displacement, the following equation should be used:
GZ = KN - KG.sin (heel angle)
(See Figure 15 below)
This enables the value of GZ to be calculated at each of the heel angles presented, and subsequently plotted as in the loading conditions presented herein.
A 5.5 Inclining Experiment Report
| Weight | Shifts | Weight | Distance | Deflections - 1 | Deflections - 2 |
|---|---|---|---|---|---|
| No. | Direction | Tonnes | Metres | mm | mm |
| 1 | > Stbd | 0.3050 | 4.8600 | 33.00 | 31.00 |
| 2 | > Stbd | 0.3050 | 4.8600 | 36.00 | 32.00 |
| 3 | > Port | 0.3050 | 4.8600 | 35.00 | 32.00 |
| 4 | > Port | 0.3050 | 4.8600 | 39.00 | 35.00 |
| 5 | > Port | 0.3050 | 4.8600 | 33.00 | 29.00 |
| 6 | > Port | 0.3050 | 4.8600 | 36.00 | 32.00 |
| 7 | > Stbd | 0.3050 | 4.8600 | 34.00 | 32.00 |
| 8 | > Stbd | 0.3050 | 4.8600 | 36.00 | 31.00 |
Pendula Lengths in Metres*: -
1) 2.115 2) 1.960
Draught Readings forward to Midships, above keel line:
Position (metres): -8.800
Draught (metres): 3.240
Position (metres): 28.800
Draught (metres) 2.040
S.G. of Water 1.0210
As inclined Condition
*One pendulum acceptable for vessels less than 24 m
Items to be removed to calculate Lightship
| Item name | Weight | LCG | VCG | FSM |
|---|---|---|---|---|
| Tonnes | Metres | Metres | Tonne.Metres | |
| Fuel (Port) | 0.92 | -2.400 | 2.030 | 0.00 |
| Fuel (Port) | 0.92 | -2.400 | 2.030 | 0.00 |
| F.W. (Fwd) | 1.12 | -0.020 | 1.030 | 0.00 |
| Electrician's Tools | 0.07 | -4.000 | 1.600 | 0.00 |
| Inclining Weights | 1.22 | 0.800 | 3.750 | 0.00 |
| Personnel | 0.23 | 0.000 | 3.000 | 0.00 |
Items to be added to calculate Lightship
| Item name | Weight | LCG | VCG | FSM |
|---|---|---|---|---|
| Tonne | Metres | Metres | Tonne.Metres | |
| Anchor & Chain | 3.800 0.00 | 9.000 | 0.30 | 0.00 |
| Liferafts | 0.15 | -5.900 | 3.900 | 0.00 |
Lightship Condition
A 5.6 Beaufort Scale of Wind Speeds and Corresponding Pressures
Table 6: Windspeed and Pressure Chart
| Beauford Number metre |
General Description | Limits of Speed in knots | Pressure kg. per sq. |
|---|---|---|---|
| 1 | Light Air | 1 to 3 | 0.02-0.2 |
| 2 | Light Breeze | 4 to 6 | 0.3 - 0.6 |
| 3 | Gentle Breeze | 7 to 10 | 0.8 - 1.7 |
| 4 | Moderate Breeze | 11 to 16 | 2.0 - 4.2 |
| 5 | Fresh Breeze | 17 to 21 | 4.8 - 7.3 |
| 6 | Strong Breeze | 22 to 27 | 8 - 12 |
| 7 | Near Gale | 28 to 33 | 13 - 18 |
| 8 | Gale | 34 to 40 | 19 - 26 |
| 9 | Strong Gale | 41 to 47 | 27 - 37 |
| 10 | Storm | 48 to 55 | 38 - 50 |
| 11 | Violent Storm | 56 to 63 | 52 - 66 |
| 12 | Hurricane | 64 and over | 68 and over |
A 5.7 Metric/Imperial Conversion Chart
| Multiply By | To Convert | To Obtain | From |
|---|---|---|---|
| 0.039370 | millimetres | inches | 25.400 |
| 0.39370 | centimetres | inches | 2.5400 |
| 3.2808 | metres | feet | 0.30480 |
| 2.2046 | kilogrammes | pounds | 0.45359 |
| 0.00098421 | kilogramme | tons (2240 lbs ) | 1016.0 |
| 0.98421 | metric tonnes of 1000 kilos | tons (2240 lbs ) | 1.0160 |
| 2.4999 | tonne per centimetre | tons per inch | 0.40002 |
| 8.2017 (M.C.T.C) | tonnes metric units (M.C.T.I) | foot ton units | 0.12193 |
| 18798 | metre radians | foot degrees | 0.0053198 |
| To Obtain | To Convert From | Multiply By |
- 10 mm cubed = 1 cubic centimetre
- 1 cubic centimetre F.W. S.G. 1.0 = 1 gramme
- 1000 cubic centimetres F.W. S.G. 1.0 = 1 kilogramme
- 1 cubic metre F.W. S.G. 1.0 = 1 tonne (1000 kilos)
- 1 cubic metre S.W. S.G. 1.025 = 1.025 tonnes
- 1 tonne S.W. S.G. 1.025 = 0.975 cubic metres
- 1 cubic metre = 35.315 cubic feet
- 1 cubic foot = 0.0283 cubic metres
A 5.8 Notes for Consultants on the Derivation of the Maximum Steady Heel Angle to Prevent Downflooding in Gusts
Figure 16: Stability Curves
HA1 = GZ1 / Cos1..3 Θf
Where:
HA1 = The magnitude of the actual wind heeling lever at 0 degrees which would cause the ship to heel to the downflooding angle (Θf) or 60 degrees
whichever is least.
GZ 1 = The lever of the ship's GZ curve at the downflooding angle or 60 degrees
whichever is least
HA2 = The mean wind heeling arm at any angle Θdegrees (= 0.5 x HA1 x COS1. 3Θ)
5.9 Notes for Consultants on the Derivation of Curves of Maximum Steady Heel Angle to Prevent Downfloowing in Squalls
The wind heeling moment is proportional to the wind pressure, and to the apparent wind speed squared. It is also dependent upon the area, height, shape and camber of the sails, the apparent wind direction and the prevailing wind gradient. As a sailing vessel heels the wind heeling moment decreases and at any heel angle (Θ ) between 0 (upright) and 90 degrees it is related to the upright value by the function: HMO = HMΘ cos 1..3 Θ where HMO is the heeling moment when upright.
The heel angle of a sailing vessel corresponds to the intersection of the heeling arm ( HA ) curve with the righting arm ( GZ ) curve, where HA = HM/Displacement.
When subjected to a gust or squall the vessel heels to a greater angle where the heeling arm curve corresponding to the gust wind speed intersects the GZ curve.
Figure 13: Stability Curves
Thus for a given heel angle a heeling arrn curve may be deduced and for a given change in wind speed the resulting change in heel angle can be predicted.
The vessel will suffer downflooding when the heeling arm curve intersects the GZ curve at the downflooding angle. This situation is illustrated in the diagram where the 'heeling arm in squall' curve intersects the GZ curve at 52 degrees. If we assume a scenario where sufficient sail is set to heel the vessel to the downflooding angle (60 degrees should be used if the downflooding angle exceeds that value) in a squall of, say 45 knots, then we can predict the wind speed which would result in any lesser heel angle in these circumstances. The upright heeling arm in the squall ( HA1 ) is derived from:
HA1 = GZf / Cos1..3Θf
If we consider a steady heel angle prior to the squall of 20 degrees we can derive similarly the corresponding value of the upright heeling arm HA2
HA2 = GZ20 / Cos1..3 20
The ratio HA2 / HA1 corresponds to the ratio of wind pressures prior to the squall and in the squall thus for a squall speed ( Vl ) of 45 knots resulting in downflooding, the wind speed prior to the squall ( V2 ) which would result in a heel angle of 20 degrees would be:
In this example, which is illustrated in the diagram,
- Θf: 52 degrees
- GZ f: 0.725 degrees
- HA1 : 1.362 degrees
- GZ 20: 0.464 metres
- HA2 : 0.503 metres
- Hence V2 : 27.4 knots
Thus when sailing with an apparent wind speed of 27.4 knots at a mean heel angle of 20 degrees, an increase in the apparent wind speed to 45 knots from the same apparent wind angle would result in downflooding if steps could not be taken to reduce the heeling moment.
These values correspond to a point on the 45 knot squall curve on page lo. which was derived from a series of such calculations using different steady heel angles. Similarly the curves for other squall speeds were derived using different values for Vl .
These calculations should be performed for both loading conditions and the results corresponding to the worst case ( i.e. the lowest maximum steady heel angles) presented in the booklet.