Pour de l'information sur les écoles de navigation de plaisance, visitez le site web ÉNP .
Table des matières
- Préambule
- Définitions
- 1. Application
- 2. Construction et résistance structurale
- 3. Stabilité
- 4. Franc-bord et marques de franc-bord
- 5. Intégrité de l’étanchéité à l’eau et de l’étanchéité aux intempéries
- 6. Dispositifs de décharge de l’eau
- 7. Circuits d’assèchement de cale
- 8. Circuits de fluide
- 9. Machines
- 10. Systèmes électriques
- 11. Appareil à gouverner
- 12. Sécurité en matière d’incendie
- 13. Équipement de sauvetage et de secours
- 14. Matériel de communication
- 15. Matériel de navigation
- 16. Ancres et chaînes
- 17. Divers équipements marins
- 18. Emménagements
- 19. Protection de personnel
- Annexe A: Specimen - Livret d'information sur la stabilite
- Section 1 - Renseignements opérationnels
- Section 2 - Données techniques et conditions de chargement
- Section 3 - Renseignements de base
Préambule
Le présent document constitue une norme non obligatoire sur la sécurité des voiliers monocoques servant à la formation dans le domaine de la navigation à voile. L’application des dispositions de la présente norme ne concerne pas les écoles de voile offrant un enseignement dans le domaine de la navigation de plaisance et du matelotage aux plaisanciers.
Les normes et la réglementation courantes sur les bateaux de type classique ne se rapportent pas à tous les aspects de la conception, de la construction et de la sécurité des voiliers-écoles. On a donc jugé opportun d’établir une norme qui tiendrait compte des caractéristiques de ce type de bateaux.
La présente norme tient compte des recherches et des travaux approfondis qu’ont effectués de nombreuses administrations, y compris la Direction maritime du ministère des Transports du R.-U. Les informations communiquées par divers intervenants au cours de l’élaboration de cette norme a également permis d’en améliorer le contenu de façon significative.
Définitions
Dans la présente norme,
« Emménagement » désigne tout compartiment situé sous un pont exposé auquel les personnes à bord ont accès à des fins autres la manœuvre du bateau. Il s’agit notamment des locaux pour l’ordinaire, le couchage et les toilettes, les cuisines et les cambuses. Les compartiments techniques du bateau ne font pas partie des emménagements.
« Équipage » désigne toute personne autre qu’un élève ou le capitaine participant à l’exploitation du bateau.
« Voilier-école en service » désigne tout voilier-école qui n’est pas neuf.
« Produit ignifuge » désigne un produit qui, appliqué sur un matériau, l'empêchera de brûler pendant une période déterminée durant laquelle les flammes ne progresseront pas et ne s’étendront pas au-delà d’une distance donnée, déterminées au cours de conditions d'essais effectués à une pression atmosphérique normale.
« Franc-bord » désigne la distance, en mètres, mesurée verticalement (de haut en bas) à partir du point le plus bas du rebord supérieur du pont supérieur jusqu’à la ligne de flottaison en eaux calmes.
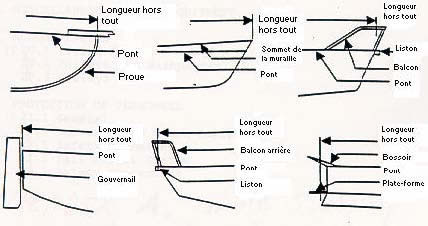
« L » ou « longueur » désigne la longueur hors tout du bateau, en mètres, mesurée à partir de l’avant de la structure permanente la plus à l'avant jusqu’à l’arrière de la structure permanente la plus à l'arrière du bateau.
Figure 1: Définition de Longueur (hors tout)
« Longueur de la ligne de flottaison » ( LLF ) désigne la distance horizontale entre le point le plus à l'avant et le point le plus à l'arrière de la ligne de flottaison mesurée avec le tirant d’eau opérationnel le plus profond.
« Nouveau voilier-école » désigne tout bateau que l’on compte utiliser comme voilier-école et dont la construction de la quille a débuté ou est terminée, ou dont la mise en rade a commencé à la date d’entrée en vigueur de la présente norme ou après cette date ou encore, tout bateau acheté et nouvellement utilisé comme voilier-école à partir de cette date.
« Voilier-école » désigne un bateau à voiles qui est exploité uniquement pour l’enseignement dans le cadre d’un programme de formation en navigation à la voile.
« Programme de formation en navigation à la voile » est un programme dispensé à bord d’un voilier dans le seul but de développer des aptitudes mentales et opérationnelles par une participation à des activités éducatives. Le programme n’a pas pour but d’améliorer uniquement les compétences en navigation à la voile.
« Élève » désigne toute personne présente à bord d’un voilier-école dans le but de participer à un programme de formation en navigation à la voile et qui n’est pas membre de l’équipage. Sur le plan légal, une telle personne n’est pas considérée comme un passager.
« Étanche à l’eau », appliqué à une structure, signifie que celle-ci empêche l’eau de la traverser, dans n'importe quel sens, sous une pression de 75 mm d’eau en un point quelconque sous le pont exposé.
« Pont exposé » désigne le pont principal ou la structure fixe qui couvre la totalité de la coque au-dessus de la ligne de flottaison opérationnelle la plus basse. Il est exposé aux intempéries et à la mer.
« Étanche aux intempéries » appliqué à une structure, signifie que celle-ci empêche l’eau de la traverser dans des conditions de mer normales.
1. Application
1.1 La présente norme s’applique à tous les voiliers-écoles monocoques canadiens qui ont plus de 15 mètres de longueur et qui servent à des fins commerciales. Les bateaux de plus petites dimensions doivent respecter le plus possible les dispositions applicables. En sus des dispositions de la présente norme, les navires neufs de 24 pi de longueur ou plus et les navires existants de 150 tonnes de jauge brute ou plus aux termes de la Convention internationale sur les lignes de charge, s’ils sont en service international, doivent se conformer aux dispositions pertinentes de la dite Convention. Ils en sont exemptés s’ils naviguent uniquement dans les Grands Lacs d’Amérique du Nord et dans le fleuve Saint-Laurent à l’est jusqu’à une ligne loxodromique tracée entre le Cap des Rosiers et West Point sur l’île d’Anticosti et, au nord de l’île d’Anticosti, jusqu’au méridien de 63 degrés de longitude ouest.
1.2 Même si la présente norme s’applique aux bateaux monocoques, on peut aussi l’utiliser pour d’autres types de voiliers-écoles.
1.3 Les propriétaires doivent s’assurer que les bateaux auxquels s’applique la norme sont construits, équipés et entretenus conformément à toutes les dispositions applicables.
1.4 La présente norme ne s’applique pas aux bateaux qui ont à bord un ou plusieurs « passagers » selon le sens donné à ce terme dans la Loi sur la marine marchande du Canada.
1.5 Le propriétaire d’un bateau doit pouvoir prouver à la satisfaction de la Division de la sécurité maritime de Transports Canada que toute personne à bord doit manœuvrer le bateau à la voile et a passé un contrat avec le propriétaire du bateau pour exercer des fonctions sur le bateau. Les personnes en question ne sont pas considérées comme des passagers sur le plan légal, et les bateaux en conformité avec les dispositions ci-dessus ne doivent pas être considérés comme des bateaux à passagers.
2. Construction et résistance structurale
2.1 Coques
2.1.1 Tous les bateaux doivent posséder une résistance structurale suffisante pour faire face aux intempéries et aux conditions de mer qu’ils sont susceptibles de rencontrer dans la région où l’on compte les exploiter.
2.1.2 La coque, la charpente, les ponts et les superstructures d’un nouveau bateau doivent être en matériaux acceptés par les inspecteurs de Transports Canada.
2.1.3 Un bateau en service a une résistance structurale suffisante s’il est en bon état et est :
- construit selon les normes prescrites par une société de classification reconnue par Transports Canada ( TC );
- d’une conception dont la sécurité a été prouvée par au moins cinq années de fonctionnement sécuritaire dans une région où les intempéries et les conditions de mer ne sont pas moins rigoureuses que celles de la région où l’on compte exploiter le bateau.
2.1.4 Dans le cas des coques métalliques, il faut tenir compte de la corrosion électrolytique et employer des moyens adéquats pour réduire au minimum ses effets. Les mesures de protection de la coque contre la corrosion doivent permettre l’utilisation du bateau en milieu marin, à moins qu’il ne soit précisé qu’il ne sera utilisé qu’en eau douce. Pour les bateaux à coque métallique, on peut utiliser un transformateur d’isolation ou un isolateur galvanique sur le conducteur de mise à la terre du câble d’alimentation électrique à quai pour réduire la corrosion galvanique.
2.2 Pont exposé
2.2.1 Le bateau doit posséder un pont exposé étanche aux imtempéries qui s’étend de l’étrave à l’arrière. Ce pont peut comporter des parties en retrait ou surélevées, à condition que ces parties soient de construction étanche aux imtempéries.
2.2.2 Dans les parties de pont en retrait, l’eau doit s’évacuer dans des conditions normales d’inclinaison et d’assiette. De plus, l’eau doit pouvoir s’évacuer lorsque le bateau gîte de 30 degrés.
2.3 Cloisons et subdivisions étanches à l’eau
2.3.1 Chaque bateau doit être pourvu d’une cloison d’abordage et de compartiments machines avec cloisons. Les petits compartiments machines peuvent être protégés par des cloisons longitudinales et transversales partielles formant une enceinte à la place de cloisons transversales intégrales.
2.3.2 La cloison d’abordage doit être située à une distance d’au moins cinq pour cent et d’au plus 10% de la longueur de la ligne de flottaison opérationnelle la plus basse à l’arrière de l’étrave. Dans le cas des bateaux ayant une étrave plus élancée, la cloison d’abordage peut être à baïonnette, la partie inférieure étant située comme précédemment, et la partie supérieure à au moins 2,5 % de la longueur de la ligne de flottaison au-dessus de la ligne de flottaison opérationnelle la plus basse.
2.3.3 Tout nouveau bateau doit être subdivisé par des cloisons étanches à l’eau disposées de façon qu'en cas d’envahissement de l’un ou de l’autre compartiment, la ligne de flottaison soit à moins de 75 mm sous un point quelconque du pont exposé. L’analyse des subdivisions doit être faite en fonction d’un bateau en charge maximale et en utilisant les valeurs de perméabilité du Règlement sur la construction de coques.
2.3.4 Il est recommandé que les bateaux auxquels s’applique la section 2.3.3 possèdent une stabilité résiduelle en phase finale d’envahissement après avarie telle que :
- l’angle d’équilibre ne dépasse pas 7 degrés par rapport à la verticale;
- la courbe résultante du bras de levier de redressement atteigne au moins 15 degrés au-delà de l’angle d’équilibre;
- le bras de levier de redressement maximal présente un radian d’au moins 0,015 m .
2.3.5 Il est également recommandé qu’aux phases intermédiaires de l’envahissement, le bras de levier de redressement maximal soit d'au moins 50 mm , avec un angle de redressement positif d’au moins sept degrés.
2.3.6 Les bateaux en service d’une longueur de 24 m ou plus doivent être conformes aux dispositions de la section 2.3.3. Ceux qui ne satisfont pas à ces exigences peuvent être acceptés par la Sécurité marine lorsqu’une évaluation des lacunes a été effectuée et que des mesures compensatoires comme les limites d’exploitation ont été prises en compte.
2.3.7 Pour les bateaux en service de moins de 24 m de longueur, il est fortement recommandé que l’on apporte les modifications qui les rendraient conformes à la section 2.3.3 au moment de la réalisation de modifications structurales importantes.
2.3.8 Les exigences de la section 2.3.3 ne sont pas obligatoires pour les bateaux ne faisant que des voyages de cabotage en eaux secondaires comme le précise le Règlement sur les voyages de cabotage, en eaux intérieures et en eaux secondaires.
2.3.9 Aux endroits où des tuyaux, des câbles, etc. pénètrent dans des cloisons étanches à l’eau, il faut installer les appareils de robinetterie et les dispositifs d’étanchéité requis.
2.3.10 Les portes des cloisons étanches à l’eau doivent également être étanches à l’eau et, sauf autorisation du capitaine, doivent être maintenues fermées en mer.
2.4 Mâts, espars et gréements
2.4.1 La conception, les matériaux et la construction des mâts, vergues, bômes, beauprés et gréements dormants, y compris les superstructures qui les supportent, doivent convenir à l’utilisation prévue et posséder une résistance suffisante pour les charges les plus élevées imposées par la voilure durant toutes les activités normales et d’urgence.
2.4.2 Il faut porter une attention particulière à l’intégration des mâts et des gréements à la structure de la coque. La structure de la coque doit être adéquatement renforcée pour assurer une résistance suffisante à la déformation des tôles.
2.4.3 Tous les gréements dormants doivent être bien fixés et leurs extrémités inférieures doivent comporter des dispositifs de réglage. Des méthodes sécuritaires et ayant fait leurs preuves peuvent être acceptées si l’inspecteur les juge appropriées.
2.4.4 Tout le gréement courant doit avoir des parcours exempts de toute obstruction grâce à l’utilisation adéquate de poulies à émerillon, de chaumards, de platines à œil, etc. Tous les composants des manœuvres courantes doivent être du type approprié et de la bonne dimension pour diminuer les risques de coincement.
2.4.5 La résistance des poulies et des manilles ainsi que de tous les ridoirs, taquets, accessoires connexes et points d’attache doit être supérieure à la résistance à la force de rupture des gréements dormants et des gréements courants associés.
2.4.6 Chaque bateau doit être pourvu de moyens adéquats pour arriser ou réduire la voilure.
2.4.7 Sauf s’il est manifeste que cela ne convient pas, chaque bateau doit soit être muni de voiles de cape séparées d’une résistance et d’une dimension suffisante, soit posséder des voiles spécifiquement conçues pour le mauvais temps.
2.4.8 En prévision de l’utilisation simultanée de voiles, il faut prévoir des moyens d’assujettissement approprié des gréements courants.
2.5 Normes de fabrication
2.5.1 La construction et l’entretien de la coque doivent être effectués dans un environnement approprié, comme le prescrit le fabricant.
2.5.2 Les coques doivent être fabriquées et entretenues dans des installations possédant l’équipement approprié pour le matériau de construction utilisé; les matériaux de construction et tout produit consomptible utilisé durant la fabrication doivent être entreposés d’une manière empêchant la corrosion ou tout autre forme de détérioration et ce, conformément à toutes les directives fournies par le fabricant.
2.5.3 La fabrication de coques en bois doit, dans la mesure du possible, être réalisée dans des locaux bien ventilés et couverts.
2.5.4 La fabrication de coques en plastique renforcé de fibres de verre doit être effectuée dans un environnement à atmosphère contrôlé où la température est maintenue, durant la fabrication, entre 15 et 21 °C , et l’humidité relative entre 40 et 80 %.
2.5.5 L’assemblage par soudage doit être réalisé par des soudeurs détenant les certificats appropriés, conformément aux normes et aux pratiques appropriées pour le matériau de construction, les procédés de soudage et l’équipement utilisés. Cette disposition n’a pas pour but d’exclure les travaux exécutés par un apprenti soudeur reconnu ou par un ouvrier métallurgiste travaillant sous la supervision d’un soudeur expérimenté.
2.5.6 Tout assemblage effectué par un moyen autre que le soudage doit être effectué par des personnes possédant les qualifications nécessaires pour la méthode employée et le matériau de construction.
3. Stabilité
3.1 Stabilité intacte
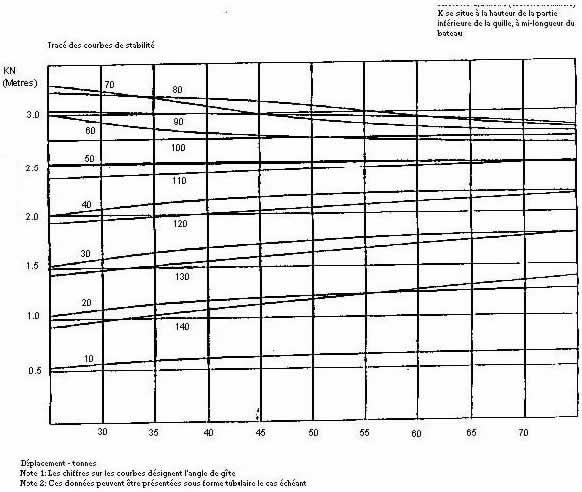
3.1.1 Le centre de gravité ( KG ) du bateau doit être établi par un essai d’inclinaison et des courbes de stabilité statique ( courbes GZ ) calculées pour les conditions suivantes :
- bateau chargé au départ avec 100 % de produits consomptibles;
- bateau chargé à l’arrivée avec 10 % de produits consomptibles.
3.1.2 Pour chacune des conditions énumérées à la section 3.1.1, la courbe du bras de levier de redressement doit avoir des valeurs positives d’au moins 90 degrés. On peut déterminer les valeurs positives minimales de la courbe du bras de levier de redressement d’un bateau d’une longueur inférieure à 24 m par la formule suivante :
90° + 25° × (24 – L ) ÷ 9
Cependant, avec une fourchette de valeurs positives inférieure à 90 degrés l’imposition de limites d’exploitation peut être nécessaire.
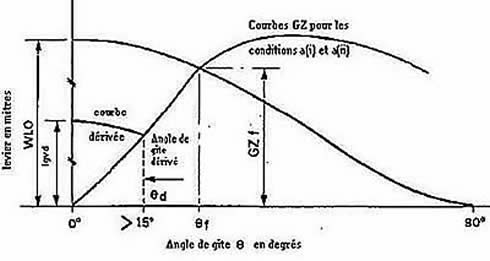
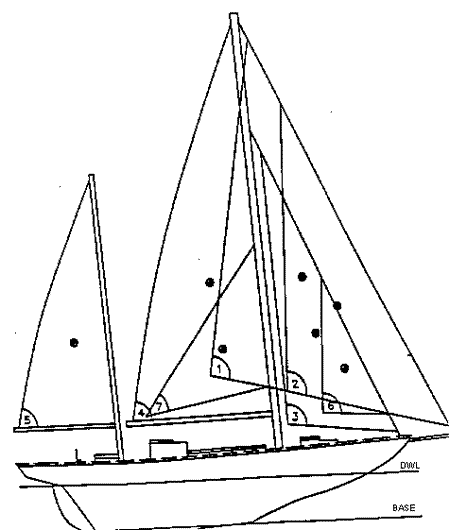
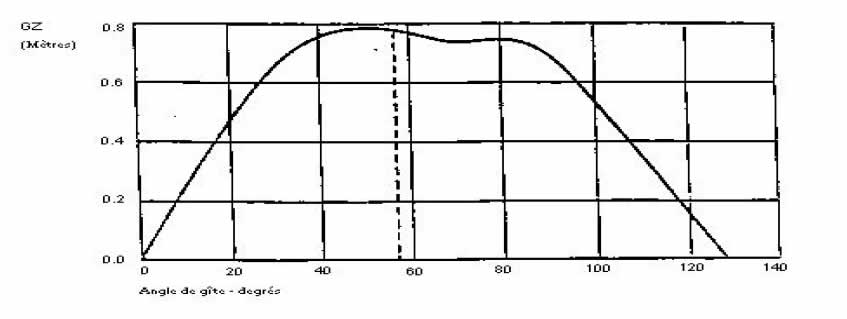
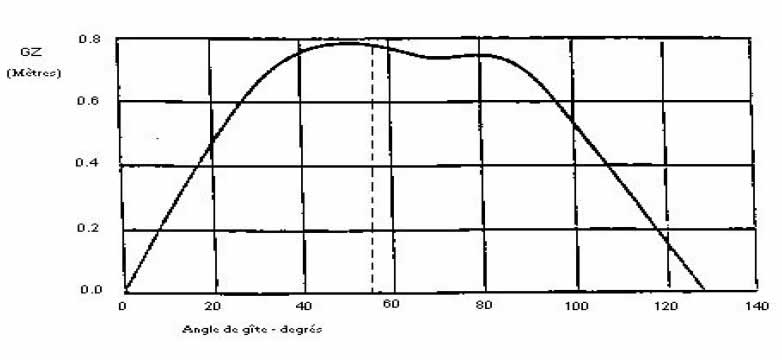
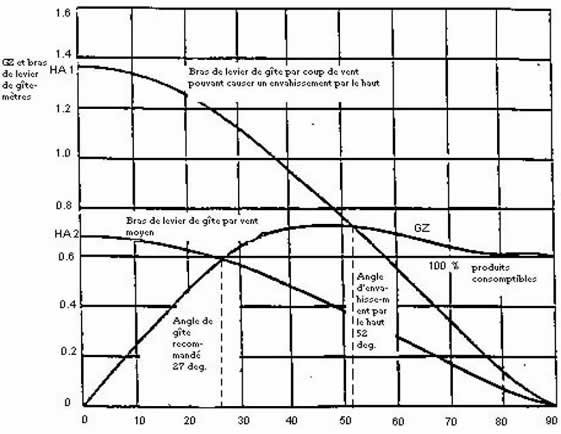
3.1.3 En outre, l’angle de gîte stable obtenu à partir de l’intersection de la courbe du « levier de gîte du vent dérivé » avec l’une des courbes GZ mentionnées à la section 3.1.1 ci-devant doit être supérieur à 15 degrés (voir la figure 1).
Figure 2 : courbes de stabilité
Dans la figure 1
lgvd = « 0,5 x WLO x Cos1..3?? Θ
où WLO = ( GZf /Cos1..3Θf)
Nota :
WLO - est la longueur du levier de gîte dû au vent réel à 0 degré qui fait gîter le bateau jusqu’à l’« angle d’envahissement par le haut » (Θ f ou 60 degrés, si cette dernière valeur est plus faible).
Si l’utilisation d’un autre angle, entre l’angle d’envahissement par le haut et 40 degrés, donne une valeur plus élevée de l’angle de gîte stable maximal, on peut utiliser cet angle au lieu de Θf .
GZf - est le levier de la courbe GZ du bateau à l’angle d’envahissement par le haut ( Θf ) ou à 60 degrés, selon l’angle le plus faible.
Θd - est l’angle auquel la courbe dérivée « d’inclinaison due au vent » fait intersection avec la courbe GZ . (Si Θd est inférieur à 15 degrés, le bateau a une stabilité suffisante aux fins de la présente norme.)
Θf - l’angle d’envahissement par le haut est atteint lorsque les ouvertures dont la surface combinée, en mètres carrés, est plus grande que
le déplacement du bateau en tonnes / 1500
sont immergées. De plus, il s’agit de l’angle auquel le bord le plus bas de l’ouverture réelle qui amènera un envahissement critique devient immergé.
3.1.4 Il faut tenir compte de toutes les ouvertures utilisées régulièrement par l’équipage et pour la ventilation lorsque l’on détermine l’angle d’envahissement par le haut. Aucune ouverture, sans égard à la dimension, pouvant mener à un envahissement progressif ne devrait être immergée à un angle de gîte de moins de 40 degrés. Cependant, il ne faut pas tenir compte des tuyaux de ventilation des citernes.
3.1.5 Si en raison de l’immersion des ouvertures d’un rouf, un bateau ne respecte pas les exigences requises, on peut ne pas tenir compte de ces ouvertures et utiliser à la place les ouvertures présentes dans le pont exposé et protégées par ce rouf pour déterminer Θf . En pareil cas, la courbe GZ doit être dérivée sans que l’on tienne compte de la poussée hydrostatique du rouf.
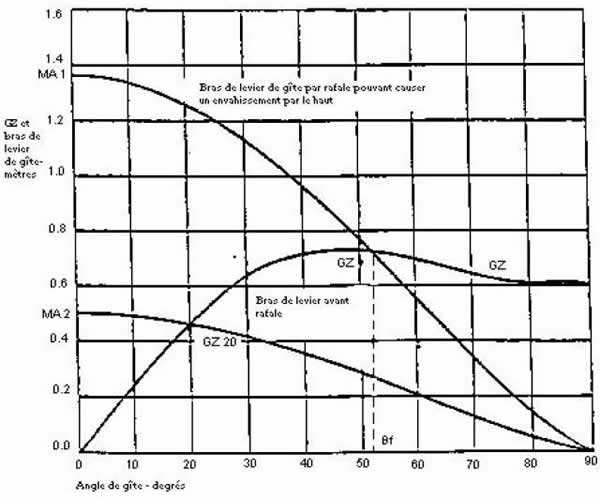
3.1.6 Si le bateau est conforme aux exigences des sections 3.1.1, 3.1.2 et 3.1.3 et s’il est appareillé en fonction d’un angle de gîte qui n’est pas plus grand que l’« angle de gîte dérivé », il devrait pouvoir résister à une rafale égale à 1,4 fois la vélocité du vent ( c.-à-d. deux fois la pression du vent) sans que des « ouvertures critiques » ne soient immergées ou qu’il ne gîte à un angle supérieur à 60 degrés.
3.1.7 Un bateau ayant un bras de levier de redressement positif inférieur à 90 degrés peut voir sa stabilité utile réduite de façon importante dans le cas où un vent qui augmente de façon constante peut occasionner un chavirement à l’angle de gîte pour lequel la courbe du bras de levier de gîte devient tangente à celle du bras de levier de redressement. Dans le cas des bateaux possédant de telles caractéristiques de stabilité, il faut inclure une note d’avertissement dans les directives de stabilité à l’intention du capitaine.
3.2 Livret d’information sur la stabilité
3.2.1 Il doit y avoir à bord, à l’intention du capitaine, un « livret d’information sur la stabilité » dont le contenu, la forme et la présentation sont basés sur le modèle de livret proposé à l’annexe 1.
3.2.2 Ce livret doit comprendre des détails concernant l’angle de gîte régulier maximal en conditions de navigation extrêmes qui devra être calculé conformément à la section 3.1.3.
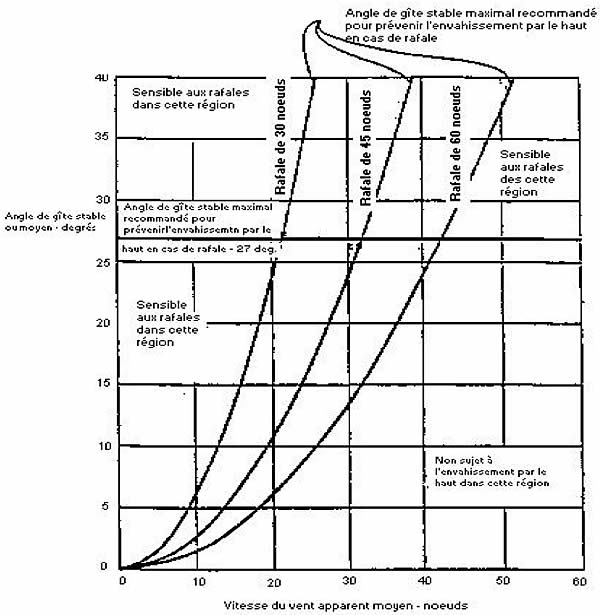
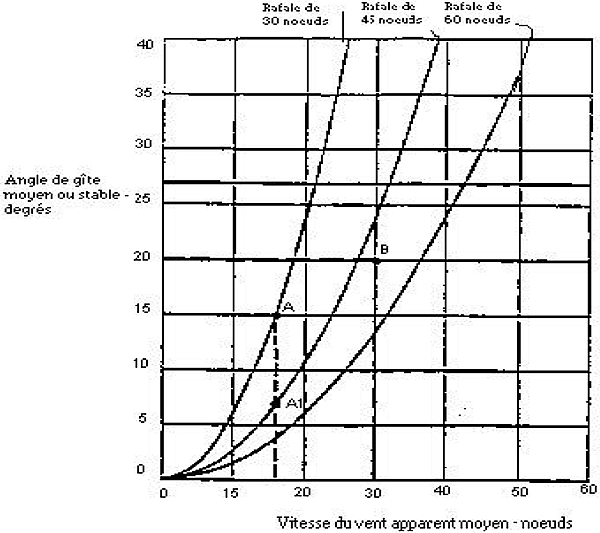
3.2.3 Le livret doit aussi donner les courbes de l’angle de gîte maximal recommandé pour prévenir l’envahissement par le haut en cas de rafale. Les détails concernant l’établissement de ces courbes sont fournis à l’annexe 1.
3.2.4 Il est recommandé qu’une copie de la partie du livret sur la stabilité traitant des courbes de l’angle de gîte stable maximal pour prévenir l’envahissement par le haut en cas de tempête soit conservé sur le bateau dans un endroit facilement accessible pour que l’on puisse le consulter rapidement.
3.3 Essai d’inclinaison
3.3.1 Il faut présenter une description générale de l’expérience portant notamment sur le personnel responsable, les conditions prédominantes, la procédure et l’équipement utilisés et, également, les précautions à prendre pour s’assurer de l’exactitude de l’expérience.
3.3.2 L’inclinaison d’un voilier doit se faire par des conditions où il y a peu ou pas de vent en raison de la prise importante du gréement dans le vent.
4. Franc-bord et marques de franc-bord
4.1 Tout bateau doit avoir une marque de franc-bord de chaque côté de la coque au milieu, correspondant au tirant d’eau maximal auquel on a déterminé sa stabilité.
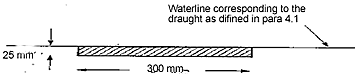
4.2 La marque de franc-bord en question, doit mesurer 300 mm de longueur et 25 mm de largeur comme l’indique la figure 2. Cette marque doit être permanente et peinte en noir sur un fond clair ou, encore, en blanc ou en jaune sur un fond foncé. Le sommet de la marque doit se situer au niveau de la ligne de flottaison correspondant au tirant d’eau mentionné à la section 4.1.
Figure 3 : marques de la ligne de flottaison
4.3 Le bateau ne doit pas être exploité dans des conditions où ses marques de franc-bord sont submergées lorsqu’il est au repos et à la verticale en eaux calmes.
5. Intégrité de l’étanchéité à l’eau et de l’étanchéité aux intempéries
5.1 Ponts
Tous les ponts exposés aux intempéries doivent être étanches à l’eau et dotés de moyens de rendre les ouvertures étanches aux intempéries (voir la section 2.2).
5.2 Écoutilles
5.2.1 Toutes les écoutilles d'un pont exposé doivent être munies d’un surbau étanche d’au moins 300 mm de hauteur. Les écoutilles donnant accès aux caissons de pont doivent être munies d’un dispositif les maintenant en position fermée.
5.2.2 Les écoutilles donnant normalement accès aux compartiments de travail doivent pouvoir s'ouvrir des deux côtés et se bloquer en position ouverte ou fermée.
5.2.3 Il est recommandé que les écoutilles soient situées sur l’axe central du bateau ou aussi près que possible.
5.2.4 Il est recommandé, en général, de garder les écoutilles fermées en mer. Il est également recommandé que les écoutilles qui doivent demeurer ouvertes pendant de longues périodes en mer soient aussi petites que possible, avec une surface maximale dégagée d’un mètre carré au sommet du surbau.
5.3 Entrées et descentes
5.3.1 Les ouvertures de portes situées au-dessus d'un pont exposé qui donnent accès à des compartiments situés au-dessous doivent être munies de surbaux d’au moins 300 mm de hauteur et les portes doivent être étanches aux intempéries.
5.3.2 Les portes en question doivent être bien construites, fixées à demeure à la cloison, ouvrir à l’extérieur et être munies d’un dispositif de fermeture qui peut être actionné de n’importe quel côté.
5.3.3 Ces portes doivent être situées aussi près que possible de l’axe central du bateau, mais si elles sont situées sur le côté d’un compartiment, les charnières doivent être du côté avant de la porte.
5.3.4 Les panneaux de descente d’un poste d’équipage ou d’un décrochement qui donnent accès à des compartiments situés au-dessous du pont supérieur doivent être munis d’un surbau dont le sommet est au moins à 300 mm au-dessus de la lisse du poste d’équipage ou de la niche de cloison. La largeur de l’ouverture de descente ne doit pas dépasser un mètre.
5.3.5 Les bateaux en service qui ne sont pas munis de surbaux adéquats doivent être dotés de bardis arrivant à une hauteur de 300 mm et doivent présenter un espace d’entreposage adjacent, visible et adéquat.
5.4 Claires-voies
5.4.1 Toutes les claires-voies doivent être étanches aux intempéries et situées sur l’axe central du bateau ou aussi près que possible. Si elles s’ouvrent, elles doivent être munies d’un surbau dépassant d'au moins 300 mm le dessus du pont et d'un dispositif d’obturation efficace.
5.4.2 Toutes ouvertures pratiquées dans un pont exposé pour des claires-voies doivent être dotées d’un verre de sécurité trempé ou d’un matériau équivalent d’au moins 6 mm d’épaisseur. Elles doivent être munies d'un couvercle amovible qui peut être fixé en place en cas de bris.
5.5 Hublots et fenêtres
5.5.1 Les hublots, les écoutillons et les fenêtres des compartiments situés au-dessous d'un pont exposé, dans un rouf ou une superstructure protégeant des ouvertures donnant sous un pont exposé doivent être du type approprié et pourvus de contre-hublots fixés à demeure et étanches aux intempéries lorsqu'ils sont fermés.
5.5.2 Sur un nouveau bateau, il ne doit y avoir aucun hublot ou aucune fenêtre dans la coque sous un pont exposé, sauf si le vitrage et le type de fixation au cadre ont une résistance équivalente à celle exigée pour la structure dans laquelle les hublots ou les fenêtres sont installés.
5.5.3 Sur un nouveau bateau, les compartiments situés sous un pont exposé ne doivent pas comporter d'écoutillons.
5.5.4 Il est recommandé que les écoutillons ne dépassent pas 250 mm de diamètre ou toute dimension équivalente.
5.5.5 Si des fenêtres doivent être installées dans des compartiments situés au-dessus d'un pont exposé et dans lesquels se trouvent des ouvertures donnant sous ce pont, ces fenêtres doivent être étanches aux intempéries. Des couvercles amovibles doivent être prévus pour la moitié des fenêtres d’une même dimension. Ceux-ci doivent assurer l’étanchéité aux intempéries lorsqu’ils sont installés à la place d’une fenêtre brisée.
5.5.6 Les hublots, les écoutillons et les fenêtres susmentionnés doivent être en vitrage de sécurité trempé ou l’équivalent d’au moins 6 mm d’épaisseur.
5.6 Ventilateurs
5.6.1 Les ventilateurs doivent être du type approprié et munis de dispositifs d’obturation fixés à demeure assurant le maintien de l’étanchéité aux intempéries.
5.6.2 Les ventilateurs doivent être installés le plus près possible du centre du bateau et leur hauteur, au bord inférieur de l’ouverture, doit dépasser le niveau d'un pont exposé d’au moins 915 mm .
5.6.3 Les ventilateurs que l’on doit laisser ouverts, p. ex. , pour l’alimentation en air des machines ou pour le refoulement de gaz nocifs ou inflammables, doivent faire l’objet d’une attention spéciale au moment du choix de leur emplacement et de la détermination de leur hauteur au-dessus d'un pont exposé étant donné qu’ils peuvent devenir des points d’envahissement par le haut.
5.6.4 Les ventilateurs doivent être situés de sorte qu’ils ne puissent pas compromettre la sûreté de fonctionnement du bateau ou dans un endroit où ils ne seront pas endommagés par l’exploitation du bateau.
5.7 Tuyaux d’air
5.7.1 Les tuyaux d’air d'un diamètre intérieur supérieur à 10 mm raccordés aux soutes de carburant ou autres citernes doivent être de type approprié et munis de dispositifs d’obturation fixés à demeure assurant le maintien de l’étanchéité aux intempéries.
5.7.2 Lorsqu’ils donnent sur un pont exposé, les tuyaux d’air doivent dépasser le niveau du pont d’au moins 300 mm et être munis d’un col de cygne.
5.8 Prises d’eau et décharges
5.8.1 Toutes les ouvertures situées sous un pont exposé doivent avoir un dispositif d’obturation efficace.
5.8.2 Lorsqu'une ouverture est située au-dessous de la ligne de flottaison, que ce soit une prise d’eau ou une conduite de décharge, elle doit être munie d’un robinet, d’une vanne ou d’un autre dispositif de fermeture facilement accessible en cas d’urgence.
5.8.3 Lorsqu'une ouverture sert au passage d'un loch ou d'un dispositif de détection que l’on peut rentrer, elle doit être étanche à l’eau et munie d’un dispositif d’obturation efficace lorsqu’un tel instrument est rentré.
6. Dispositifs de décharge de l’eau
6.1 Tout pont supérieur muni d’un plat-bord ou d’un pavois pouvant retenir temporairement de l’eau embarquée sur le pont doit être muni d’un nombre adéquat de sabords de décharge.
6.2 La surface totale des sabords de décharge doit représenter au moins 10 pour cent de la surface du plat-bord ou du pavois qui s’étendent sur les deux tiers du bateau à mi-longueur. Un sabord de décharge doit être situé dans le tiers inférieur du plat-bord ou du pavois, aussi près que possible du pont.
6.3 Les sabords de décharge de plus de 300 mm de profondeur doivent avoir des barreaux espacés d’au plus 230 mm ou d’autres dispositifs de protection appropriés. Si les sabords de décharge sont munis d’obturateurs, la partie supérieure de ces derniers doit être articulée pour qu'ils puissent s'ouvrir de l’extérieur. Les charnières de l’obturateur doivent avoir des tiges ou des paliers en matériau non corrosif.
6.4 Les structures et les compartiments situés au-dessus du pont supérieur non étanches aux intempéries doivent être munies de dispositifs d’écoulement efficaces.
7. Circuits d’assèchement de cale
7.1 Tout bateau doit être équipé d’un circuit d’assèchement à auto-amorçage efficace qui comprend au moins :
- si sa longueur est inférieure à 20 m , une pompe de cale manuelle d’une capacité minimale de 1 m³/h et une pompe de cale fixe actionnée par moteur ou autonome d’une capacité minimale de 5 m³/h ;
- si sa longueur est supérieure ou égale à 20 m, deux pompes à moteur fixes d’une capacité minimale combinée de 10 m³/h .
7.2 Les pompes et la tuyauterie doivent être disposées de façon que l’on puisse assécher tout compartiment et qu’il soit possible de procéder à la révision d’une pompe sans mettre les autres pompes de cale hors service.
7.3 Dans le cas des bateaux en service qui ne satisfont pas aux exigences présentées aux sections 7.1 et 7.2, il faut prévoir d'autres moyens qui permettent d'assurer un niveau de sécurité suffisant.
7.4 Les pompes portatives ne doivent pas peser plus de 20 kg .
7.5 Les compartiments desservis par un circuit d’assèchement de cale permanent doivent être dotés de prises d’aspiration disposées de façon à permettre d'évacuer l'eau lorsque le bateau est incliné de 15 degrés d’un côté ou de l’autre.
7.6 Les pompes de cale raccordées ou que l’on peut raccorder au circuit d’assèchement doivent pouvoir fonctionner efficacement lorsque le bateau est incliné de 30 degrés d’un côté ou de l’autre.
7.7 La tuyauterie d’assèchement installée à demeure doit être disposée de manière à prévenir le transfert de l’eau d’envahissement d’un compartiment à un autre.
7.8 Toute la tuyauterie d’assèchement doit être lisse et avoir un diamètre d’au moins 25 mm ; les prises d’aspiration doivent avoir une crépine.
7.9 Les pompes portatives, leur source d’alimentation et les flexibles doivent être rangés dans des compartiments clairement identifiés et maintenus en place grâce à des dispositifs de fixation à dégagement rapide.
7.10 Tous les clapets d’aspiration et les clapets de refoulement des pompes des nouveaux voiliers-écoles doivent être de type antiretour blocable. La tuyauterie d’assèchement doit aussi être clairement identifiée, et toutes les commandes d’aspiration doivent identifier clairement le compartiment desservi.
7.11 Les conduites de décharge traversant la coque doivent être munies d'un clapet antiretour ou d’un syphon à la hauteur du passage de coque.
8. Circuits de fluide
8.1 Tous les réservoirs permanents pouvant contenir un fluide doivent être situés sur l’axe central longitudinal ou aussi près de ce dernier que possible, orientés longitudinalement et placés le plus bas possible dans le bateau. Il est recommandé que les réservoirs à carburant soient pourvus de cloisons/chicanes pour réduire au minimum l’effet de carène liquide.
8.2 Tous les réservoirs permanents doivent être appuyés à la charpente du bateau et y être fixés solidement, en tenant compte des contraintes en matière de charges dynamiques, de dilatation différentielle et de corrosion électrolytique.
8.3 Le matériau constitutif des réservoirs et de tous les composants d’un circuit de fluide doit être compatible avec le fluide contenu pour éviter toute corrosion des réservoirs et des composants connexes, et toute détérioration de la qualité du fluide.
8.4 Les joints des circuits de fluide doivent être fermement maintenus en place par des moyens approuvés et appropriés au matériau de construction.
8.5 Les composants des circuits de fluide nécessitant un entretien ou une inspection périodiques doivent être facilement accessibles.
8.6 Les raccords des réservoirs doivent être munis d'un clapet ou d'un robinet pour permettre l’arrêt des fuites ou la dépose de composants.
8.7 Les composants des circuits de fluide doivent supporter une pression de sécurité de 1,5 fois la pression de service maximale normale; il faut tenir compte de toute charge statique à l’intérieur du circuit.
8.8 Les réservoirs permanents contenant des produits consomptibles doivent être pourvus de prises de chargement et de bouchons de remplissage étanches clairement identifiés.
8.9 Les réservoirs permanents doivent être pourvus de dispositifs de mise à l’air libre, conformément aux sections 78 à 89, Division II, Partie I de l’annexe XV du Règlement sur les machines des navires.
8.10 Les conduites de décharge d’« eaux grises » doivent être dotées de dispositifs de passage de coque munis d'un clapet antiretour ou d'une vanne d’arrêt.
8.11 Tous les tuyaux installés dans lesquels passe un fluide ou tous les tuyaux de mise à l’air libre raccordés aux réservoirs de carburant ou d'eaux-vannes, installés en permanence doivent être situés le plus loin possible des locaux habités et des aires de travail habituelles. Les mises à l’air libre des réservoirs doivent être munies à la sortie d'un pare-flammes en matériau non corrosif.
8.12 Toutes les conduites d'évacuation doivent présenter une pente minimale de 5 % vers le raccord du réservoir, sauf si elles sont reliées à un système d’aspiration.
9. Machines
9.1 Moteurs à combustion interne
9.1.1 Les nouveaux bateaux doivent être dotés d’un moteur diesel marin et avoir des réserves de carburant suffisantes pour disposer d’une autonomie d’au moins 24 heures sur une mer calme, à une vitesse minimale de 6 noeuds. Les bateaux dotés de moteurs utilisant d’autres types de carburant doivent être soumis à un examen spécial du Conseil maritime relativement à la prévention des incendies.
9.1.2 Les assises et dispositifs de fixation des moteurs ainsi que les composants de la structure de support doivent être conçus en fonction des charges qui résultent d’une accélération de 2 g dans l’une ou l’autre direction jusqu’à un angle de gîte de 60 degrés.
9.1.3 La conception des moteurs et leur disposition sur le bateau doivent permettre un fonctionnement sans restrictions, à un angle de gîte de 15 degrés. Les machines doivent être conçues pour fonctionner lorsque le bateau est en position verticale et lorsqu’il gîte, d’un côté ou de l’autre, de 15 degrés ou moins dans des conditions statiques et de 22,5 degrés dans des conditions de roulis, tout en étant incliné de 7,5 degrés vers l'avant ou vers l’arrière dans des conditions de tangage.
9.1.4 La façon dont sont installés les moteurs doit permettre d'accéder sans restriction et rapidement à tous les points de ravitaillement, aux organes de raccordement des circuits et aux filtres.
9.1.5 Tous les raccords des circuits de fluide aux moteurs doivent être munis de robinets ou de vannes sur le côté de la coque pour permettre la dépose du moteur.
9.1.6 L’espace sous le moteur doit être prévu pour contenir les fuites de fluide et faciliter l'élimination du liquide accumulé.
9.1.7 L'installation des moteurs ne doit pas gêner l'alimentation en liquide de refroidissement et en air comburant, conformément aux recommandations du fabricant du moteur.
9.1.8 L’air comburant et l’air de refroidissement doivent être canalisés à partir du pont supérieur, les conduits étant conçus pour réduire au minimum l’aspiration d’embruns ou d’humidité.
9.1.9 L’air de ventilation et l’air de refroidissement doivent être acheminés par des conduits séparés de même section transversale pour l’entrée et la sortie. Lorsque l’air comburant provient de l’intérieur du compartiment machines, la section transversale du conduit d’admission d’air doit être proportionnellement plus grande.
9.1.10 Tous les conduits d’air de ventilation et d’air comburant doivent être adéquatement supportés et, dans la mesure du possible, ne devraient pas traverser les emménagements.
9.1.11 La section transversale des conduits d'admission et d'extraction fournissant seulement l’air de ventilation/refroidissement doit être d’au moins 22 centimètres carrés pour chaque mètre de largeur du bateau.
9.1.12 Chaque moteur doit être doté d’un régulateur de vitesse et d’un dispositif d’arrêt. L’instrumentation doit se trouver à l’endroit d'où le moteur est normalement commandé. Elle doit permettre un contrôle des paramètres spécifiés par le fabricant du ou des moteurs avec les restrictions indiquées par ce dernier. Il faut aussi prévoir des dispositifs d’alerte visuelle et sonore au cas où une défectuosité de l’instrumentation entraînerait une panne de moteur.
9.1.13 Les moteurs qui sont normalement contrôlés et commandés à distance doivent être dotés de dispositifs locaux de contrôle et de commande.
9.1.14 Les pièces mobiles, les surfaces chaudes et les autres sources de danger doivent être installées et protégées de façon à réduire au minimum tout danger pour les personnes à bord.
9.1.15 Les tuyaux d’échappement doivent être aussi courts que possible. Les passages de cloison ou de coque du bateau doivent être adéquatement isolés. Aucun tuyau d’échappement sec ne doit traverser les emménagements.
9.1.16 Aucun tuyau d’échappement sec ne doit aboutir à moins d’un mètre d'un pont exposé, d’une prise de ventilation ou d’une embarcation de secours.
9.1.17 Il faut prévoir une communication bi-directionnelle entre les compartiments contenant les moteurs de propulsion et le poste d'où on gouverne normalement le bateau, sauf si l’expert considère que cela n’est pas pratique.
9.1.18 Il faut pouvoir démarrer tous les moteurs installés à demeure à partir de l’arrêt complet lorsque le bateau se trouve à quai.
9.1.19 Les moteurs de propulsion doivent être installés dans des compartiments fermés qui doivent, dans la mesure du possible, être étanches à l’eau, et toute cloison d'un local habité contigu doit être résistante au feu et étanche aux vapeurs (voir la section 12.4.8).
9.1.20 L’équipement électrique installé dans un compartiment machines fermé doit être sécuritaire ou à sécurité intégrée à cause de l’environnement dangereux auquel il peut être exposé.
9.2 Transmission et lignes d’arbres
9.2.1 L’énergie développée par les moteurs de propulsion doit être transmise par une transmission et une ligne d’arbres conçues et installées conformément aux règlements d'une société de classification reconnue par TC ou ayant fait leurs preuves en matière de sécurité sur une installation similaire utilisée pendant au moins cinq ans.
9.2.2 Les transmissions doivent permettre la propulsion en marche avant et en marche arrière et doivent être dotées d’un point mort.
9.2.3 La commande de la transmission doit être adjacente aux commandes du moteur qui l’entraîne.
9.2.4 Aucune ligne d’arbres ne doit pénétrer dans les locaux habités.
9.2.5 Les lignes d’arbres doivent être conçues et installées de façon que le régime critique débute à au moins 110 % du régime maximal nominal.
9.2.6 Les points de passage de la ligne d’arbres dans la coque doivent être munis de presse-étoupes d’étambot et de paliers conformes à l’usage établi et doivent être dotés des mécanismes de réglage et de lubrification appropriés.
10. Systèmes électriques
10.1 Généralités
10.1.1 Les installations électriques doivent être conçues pour réduire au minimum les risques d’incendie et d’électrocution. Il faut porter une attention spéciale à la protection contre les courts-circuits et les surcharges sur tous les circuits, sauf les circuits de lancement des moteurs qui sont alimentés par des batteries.
10.1.2 Lorsque l’éclairage général du bateau est assuré par un système électrique centralisé, on doit prévoir une autre source d’éclairage, p. ex. des lampes alimentées par des batteries ayant une puissance suffisante pour permettre aux personnes de gagner le pont.
10.1.3 Dans la mesure du possible, il faut séparer les composants électriques, les câbles et les fils de systèmes dont les caractéristiques électriques diffèrent. Il faut en outre indiquer la tension des circuits au point d’origine ou au point d’arrivée.
10.1.4 Les câbles, les connecteurs et les bornes doivent être choisis en fonction de leurs capacités conductrices; tous les câbles de moins de 55 volts doivent être faits de conducteurs toronnés en cuivre et munis d’un isolant ininflammable et être d’une catégorie commerciale pouvant être utilisée à moins 75 °C . Les câbles de plus de 55 volts doivent être d’un type marin approuvé par TC .
10.1.5 Tous les circuits électriques doivent être protégés individuellement contre les surintensités par des fusibles ou des disjoncteurs appropriés; les disjoncteurs c.a. et c.c. doivent être à déclenchement libre et à réarmement manuel.
10.1.6 Tous les composants et fils électriques exposés aux intempéries doivent être imperméables et d'un matériau non corrosif. Les passages de câbles dans la structure du pont doivent être munis de connexions étanches à l’eau.
10.1.7 Les sources d’alimentation électrique des feux de navigation, des systèmes de gouverne ou du circuit de chargement des batteries doivent être jumelées à un indicateur de fonctionnement visuel au poste de commande.
10.1.8 La fonction de tous les interrupteurs, fusibles et disjoncteurs doit être indiquée.
10.1.9 Les coffrets ou les boîtiers des dispositifs électroniques et des radios ainsi que les connexions des réservoirs de carburant et de remplissage des réservoirs doivent être raccordés au côté négatif du système électrique. Les conducteurs de raccordement doivent être en bronze ou en cuivre.
10.1.10 Les fils électriques doivent, autant que possible, éviter les compas ou les composants du système de compas. Si cela est inévitable, les fils c.c. doivent être à paires torsadées et installés selon les recommandations du fabricant du compas.
10.1.11 Des conducteurs de paratonnerre doivent être installés sur chaque mât des bateaux non métalliques et des bateaux en aluminium ou en acier ayant des mâts ou des mâts de hune en bois, sauf dans les endroits où la hauteur d’une antenne dépasse celle des mâts et où l’antenne est dotée d'un déchargeur de foudre ou d’un autre dispositif.
10.1.12 Les conducteurs de paratonnerre doivent être en un feuillard de cuivre continu ou un câble d’au moins 25 mm² ( n° 4 AWG ) de section et doivent être continus à partir d’un point situé 150 mm au-dessus de la pomme du mât jusqu’à une plaque de cuivre d’au moins 0,2 m² de surface fixée à la quille, sous la ligne de flottaison, en un point où elle restera immergée dans toutes les conditions de gîte et d’assiette. On ne doit utiliser la plaque du conducteur de foudre que pour protéger le bateau de la foudre.
10.2 Circuits c.c.
10.2.1 Les circuits c.c. doivent être bifilaires avec une alimentation et un retour isolés; les circuits de plus de 55 volts doivent être conformes à la publication TP 127.
10.2.2 Si les moteurs installés dans les bateaux à coque non métallique sont isolés électriquement de la coque, tous les blocs-moteurs peuvent être utilisés comme masse commune pour l’équipement électrique monté sur le moteur.
10.2.3 Les parties métalliques non conductrices exposées de l’équipement électrique doivent être mises à la masse par la coque; dans le cas des bateaux en bois ou en plastique renforcé, cette mise à la masse doit être effectuée par l’intermédiaire d’un conducteur continu aboutissant au moteur principal ou à une plaque de mise à la masse en cuivre d’au moins 0,2 m² de surface, fixée à la quille, sous la ligne de flottaison, en un point où elle est complètement immergée dans toutes les conditions de gîte.
10.2.4 Toutes les connexions de mise à la masse doivent être en cuivre, facilement accessibles, fixées solidement et protégées, au besoin, contre les dommages et la corrosion électrolytique.
10.2.5 Dans le cas des systèmes de distribution le côté relié à la masse doit être de polarité négative.
10.2.6 Les panneaux et les tableaux de distribution électrique doivent être situés dans des zones bien ventilées, protégées de la pluie ou des embruns qui peuvent pénétrer par les écoutillons, les ouvertures de mise à l’air libre et des ponts.
10.2.7 Le tableau ou le tableau de distribution c.c. doit comporter un voltmètre, un ampèremètre et un voyant de charge des batteries.
10.2.8 Le panneau ou le tableau de distribution c.c. doit également indiquer quels circuits du bateau sont alimentés en courant. Cela peut se faire au moyen d’interrupteurs avec voyants incorporés.
10.3 Entreposage des batteries
10.3.1 Les installations d’entreposage des batteries doivent être bien étiquetées et doivent indiquer le danger qu’elles comportent.
10.3.2 Les batteries ne doivent pas se déplacer de plus de 25 mm lorsqu’une force de traction de 40 kg ou équivalant à deux fois leur poids, selon la valeur la moins élevée, est appliquée sur leur centre de gravité durant une minute dans chacune des cinq directions suivantes :
- à la verticale;
- à l’horizontale, vers l’avant et vers l’arrière;
- à l’horizontale, vers bâbord et vers tribord.
10.3.3 Il est interdit d'installer une batterie directement au-dessus ou au-dessous d’un réservoir à carburant, d’un filtre ou d’un raccord de canalisation à carburant.
10.3.4 Il est interdit d'installer les batteries dans les locaux habités ou dans les compartiments contenant des produits inflammables. Il est recommandé de ne pas installer les batteries dans les compartiments machines, sauf si des mesures adéquates sont prises pour disperser les gaz produits au moment de la charge; il est recommandé également d’installer les batteries servant au démarrage du moteur à côté du moteur pour réduire la longueur des conducteurs.
10.3.5 Les canalisations à carburant métalliques et les composants métalliques du circuit d’alimentation en carburant situés au-dessus d’une batterie installée doivent être protégés par un matériau diélectrique.
10.3.6 Les batteries doivent être installées de façon qu’aucun objet métallique ne puisse entrer en contact avec les bornes non mises à la masse.
10 3.7 Les différents types de batteries ou celles utilisant des électrolytes différents doivent être fixées en place dans des compartiments séparés.
10.3.8 L’une des inscriptions suivantes doit être marquée sur la borne positive de la batterie ou sur le bac contenant celle-ci, près de la borne :
- « POS »;
- « P »;
- « + ».
10.3.9 Aucun conducteur ne peut être raccordé aux bornes d’une batterie au moyen d’un connecteur à ressort.
10.3.10 Les batteries ventilées raccordées à un dispositif de charge d'une puissance de sortie de plus de 2 kW doivent être logées dans un compartiment adéquatement ventilé et réservé uniquement aux batteries ou, encore, peuvent être installées dans un boîtier approprié, sur le pont.
10.3.11 Les batteries ventilées raccordées à un dispositif de charge d'une puissance de sortie comprise entre 0,2 et 2 kW doivent être installées conformément aux exigences de la section 10.3.10 ou, dans un boîtier, à l’intérieur d’un compartiment machines bien ventilé ou dans un compartiment semblable.
10.3.12 Les parties intérieures de tous les compartiments pour les batteries ventilées, à savoir les caisses à claire-voie, les caisses de groupement, les boîtiers, les tablettes et autres composants structuraux doivent être faits d’un matériau résistant à la corrosion et, le cas échéant, recouverts d'une peinture ou d'un matériau de revêtement appropriés.
10.3.13 Il faut prévoir un moyen de ventilation des compartiments et les boîtiers pour batteries, conformément à la sous-section 10.3.14, pour prévenir toute accumulation de gaz inflammables dangereux pouvant survenir durant les cycles de charge et décharge. Il faut aussi prendre en considération la protection de la ou des batteries contre les conditions environnementales.
10.3.14 Il est permis d'avoir une ventilation naturelle pour les batteries si les conduits passent directement du haut du compartiment ou du boîtier à l’air ambiant au-dessus de ces derniers et qu’aucune des parties des conduits n’est inclinée à plus de 45° par rapport à la verticale; s’il n’est pas possible de recourir à une ventilation naturelle, une ventilation mécanique est exigée lorsque la quantité d’air expulsé est au moins égale à :
Q = 110 × I × N
Où :
N = nombre d'éléments en série
I = intensité maximale au dispositif de charge durant la formation de gaz, mais pas moins de 25 % de l’intensité maximale que l’on peut obtenir (en ampères)
Q = quantité d’air expulsée en litres/h
10.3.15 Les batteries connectées en permanence aux systèmes électriques du bateau doivent être munies d’un circuit de charge qui doit comprendre des dispositifs empêchant l’inversion de polarité du circuit de charge et la décharge des batteries par le circuit de charge.
10.3.16 Les batteries installées en permanence qui peuvent subir un emballement thermique doivent être dotées d’un dispositif d’alarme de température qui déclenche un signal sonore distinct. Les circuits de charge doivent comporter des sectionneurs ou des disjoncteurs.
10.3.17 Il faut prévoir des sectionneurs pour mettre hors tension toutes les batteries installées en permanence du système de distribution du bateau.
10.4 Circuits c.a.
10.4.1 Les caractéristiques importantes des systèmes auxquelles réfère la présente norme sont : un système bifilaire monophasé de 120 V , 60 Hz , un système trifilaire monophasé de 120/240 V , 60 Hz , avec neutre mis à la masse et un système trifilaire triphasé non mis à la masse.
10.4.2 Le système doit être polarisé et les conducteurs identifiés de la même façon :
- conducteurs de masse isolés – verts;
- conducteurs non mis à la masse – noirs ou rouges ou les deux;
- neutre – blanc.
10.4.3 Il faut raccorder les conducteurs de masse à un seul point de mise à la masse, à savoir le tableau de distribution principal.
10.4.4 Les circuits doivent être conçus pour ne pas pouvoir être alimentés simultanément par plus d’une source d’énergie.
10.4.5 Les connecteurs d’alimentation à quai doivent être étanches aux intempéries.
10.4.6 Le câble reliant la prise d’alimentation à quai au panneau de distribution ou au tableau de distribution doit être protégé par un disjoncteur ou par un interrupteur à fusible situé à moins de 3 m à bord, à partir du raccordement quai-navire. Un indicateur de polarité pour les circuits c.c. ou les circuits c.a. monophasés ou un indicateur de séquence pour courant triphasé doit être installé sur la prise d’alimentation à quai ou sur le tableau de distribution.
10.4.7 Tous les conducteurs d’alimentation des générateurs de bord ou quai-navire doivent être protégés de la manière suivante contre les surintensités par des disjoncteurs :
- alimentation monophasée de 120 V – les deux conducteurs sans mise à la masse;
- alimentation monophasée de 120/240 V et de 240 V – les deux conducteurs sans mise à la masse;
- alimentation triphasée de 120/240 V et 120/208 V – tous les conducteurs sans mise à la masse.
10.4.8 Chaque circuit de dérivation de 55 volts ou plus doit comporter un interrupteur ou un disjoncteur avec une borne pour chaque conducteur; les interrupteurs ou disjoncteurs installés doivent ouvrir/fermer simultanément le circuit du conducteur mis à la masse et le circuit du conducteur isolé.
10.4.9 Les fusibles ou les disjoncteurs ne doivent pas dépasser l’intensité nominale du plus petit conducteur du circuit; les moteurs doivent être protégés par des dispositifs sensibles à l’intensité.
10.4.10 Dans le cas des systèmes de distribution avec neutre mis à la masse, on peut utiliser des interrupteurs de circuit en cas de fuite à la masse sur les circuits monophasés pour protéger le personnel et l’équipement; pour protéger l’équipement, on peut utiliser des disjoncteurs de fuite à la masse.
10.4.11 Il faut protéger le primaire des transformateurs contre les courts-circuits. La protection des transformateurs contre les surcharges peut être assurée par des dispositifs, raccordés soit au primaire, soit au secondaire, ou par des dispositifs d'une valeur de consigne inférieure à 125 % de l’intensité nominale du primaire ou du secondaire.
10.4.12 Le circuit de dérivation bifilaire ne doit pas alimenter des points qui dépassent 80 % de la valeur de consigne du dispositif de protection du circuit de dérivation.
10.4.13 Le panneau ou tableau de distribution c.a. doit être doté d’instruments indiquant la tension et l’intensité de la génératrice afin que l’on puisse contrôler l’état de l’isolement par rapport à la masse.
10.4.14 Sur les systèmes de 120 V ou plus, il faut vérifier la résistance de l’isolant des câbles une fois leur installation terminée.
10.5 Alimentation électrique de secours
10.5.1 Dans tout bateau, la capacité des batteries doit être suffisante pour alimenter simultanément l’équipement suivant durant 12 heures :
- l’éclairage de sécurité sur le pont supérieur aux endroits où sont déployés les embarcations de sauvetage et aux zones d’embarquement;
- l’éclairage de sécurité de chaque sortie utilisée comme moyen principal d’évacuation vers le pont supérieur;
- l’éclairage du compas;
- un émetteur-récepteur, pour une transmission d’une durée totale de 30 minutes;
- tout dispositif de détection automatique des incendies ou tout matériel d’extinction dont le fonctionnement est tributaire d’une source d’alimentation électrique;
- quand cela est exigé par le Règlement sur les abordages, le tableau des feux de route.
Dans le cas de bateaux effectuant régulièrement des voyages de courte durée, une durée d’alimentation inférieure à 12 heures peut être acceptée.
10.5.2 Les exigences énoncées à la section 10.5.1 peuvent être satisfaites par des batteries locales installées de façon à en assurer un rendement optimal.
11. Appareil à gouverner
11.1 Il est recommandé que le poste de gouverne principal soit situé de façon que la personne qui manœuvre le gouvernail ait une bonne visibilité pour naviguer de façon sécuritaire. Il est aussi recommandé de doter ce poste d’un volant ou d’une barre de gouvernail disposés de façon à permettre une amplitude de mouvement complète, sans obstruction.
11.2 Le safran doit être conçu et situé de façon à optimiser l’efficacité de la gouverne en toutes circonstances, y compris à des angles de gîte allant jusqu’à 60 degrés.
11.3 Tous les appareils à gouverner, les câbles de commande, les cordages ou les tiges et les poulies ou réas doivent être disposés et protégés pour réduire au minimum les risques de coincement avec des objets mobiles, tout en étant facilement accessibles pour les inspections ou la lubrification.
11.4 Même si l’appareil à gouverner est assisté, on doit pouvoir l’utiliser manuellement. Un dispositif d’avertissement doit indiquer toute panne du dispositif de gouverne assisté au poste de barre.
11.5 Tous les accessoires et les fixations des composants de l’appareil à gouverner doivent avoir une résistance adéquate, en tenant compte des charges associées à l’utilisation d’un servomoteur ou à un mécanisme de démultiplication.
11.6 En cas de panne occasionnant la perte de l’appareil à gouverner principal, il doit y avoir un moyen de gouverner de secours. Les instructions pour l’installation et l’utilisation de l’appareil à gouverner de secours doivent être affichées près du poste de barre.
11.7 Il doit être possible, avec le système de gouverne principal, de faire passer le safran de 35 degrés d’un côté à 35 degrés de l’autre côté lorsque le bateau est à son tirant d’eau de haute mer le plus profond et qu’il évolue en marche avant à la vitesse de service maximale.
11.8 Si le système de gouverne principal est assisté, il doit pouvoir faire passer le safran de 35 degrés de n’importe quel côté à 30 degrés de l’autre côté en moins de 28 secondes lorsque le bateau est à son tirant d’eau de haute mer le plus profond et qu’il évolue en marche avant à la vitesse de service maximale.
11.9 La pression nominale utilisée dans le calcul de l’échantillonnage de la tuyauterie et des autres composants de l’appareil à gouverner soumis à une pression hydraulique interne doit être d’au moins 1,25 fois la pression de service maximale prévue pour les conditions opérationnelles spécifiées à la section 13.7, en tenant compte de toute pression pouvant exister du côté basse pression du système. Un calcul de fatigue peut être nécessaire pour la conception des composants de la tuyauterie; il faudra tenir compte des pressions pulsatoires inhérentes aux charges dynamiques si l’inspecteur de TC l’exige.
12. Sécurité en matière d’incendie
12.1 Généralités
12.1.1 Dans la mesure du possible, tous les matériaux utilisés dans la construction de la coque, les surfaces de finition, les revêtements de ponts et les garnitures extérieures doivent avoir un indice de propagation de la flamme peu élevé.
12.1.2 La partie située sous le pont immédiatement sous les postes d’arrimage des embarcations de sauvetage et les cloisons adjacentes doivent être protégées avec un isolant ayant un degré de résistance au feu de 30 minutes.
12.1.3 Les accès pouvant être utilisés comme moyen d’évacuation vers le pont doivent être construits selon la norme B-15, comme le prescrit le Règlement sur la construction de coques.
12.1.4 Aucun matériau qui émet des quantités excessives de fumée et de gaz toxiques lorsqu’il est exposé à des températures supérieures à 60 °C ne doit être employé dans la construction, l’ameublement ou la décoration des locaux habités.
12.1.5 Nonobstant les dispositions de la section 12.1.1, les bateaux en service peuvent conserver tout composant en bois présent dans les locaux habités.
12.1.6 Les bateaux doivent être dotés d’au moins une pompe à incendie actionnée par une unité de propulsion ou une source d’énergie indépendante et également d’un collecteur d’incendie, de bouches d’incendie, de manches à incendie et de lances d’incendie.
12.1.7 Le nombre de bouches d’incendie doit être suffisant et chacune doit être pourvue d’un tuyau. Elles doivent être réparties de façon qu’il soit possible d’arroser suffisamment toutes les parties du bateau.
12.1.8 Les pompes à incendie peuvent aussi être utilisées comme pompes de cale.
12.1.9 Le collecteur d’incendie, les branchements d’eau généraux et les bouches d’incendie doivent être construits de sorte qu’ils ne se corroderont pas, qu’ils ne seront pas rendus inefficaces par la chaleur et qu’ils seront protégés contre le gel.
12.1.10 Les bateaux doivent posséder une pompe à incendie située à l’extérieur du compartiment machines et ayant une capacité d’au moins 1,1 m³/h . Celle-ci doit être munie d’un tuyau d’aspiration et d’un tuyau de refoulement appropriés pour la lutte contre l’incendie.
12.1.11 Les conduits acheminant des vapeurs ou des gaz dont la température dépasse 60 °C , doivent être adéquatement isolés à la hauteur des passages de cloison ou de pont.
12.1.12 Les conduits acheminant des vapeurs ou des gaz inflammables ou toxiques doivent être faits d’un matériau incombustible et doivent être supportés et retenus de façon appropriée.
12.1.13 Dans la mesure du possible, les composants électriques et les composants qui contiennent un fluide inflammable doivent être le plus éloignés possible les uns des autres.
12.1.14 Tout l’équipement de détection et d’extinction d’incendie qu’exige la présente norme doit être approuvé par une autorité reconnue nationalement dans ce domaine et doit être conforme au Règlement sur le matériel de détection et d’extinction d’incendie.
12.2 Locaux d’habitation
12.2.1 Les locaux utilisés pour l’ordinaire et les postes de couchage doivent être équipés de détecteurs de fumée et de détecteurs de monoxyde de carbone à alarme sonore.
12.2.2 Le bateau doit posséder à son bord au moins un extincteur à mousse de 4,5 L approuvé par les Laboratoires des assureurs du Canada ( ULC ), rangé dans un endroit identifié de façon bien visible, dans chaque compartiment utilisé pour l’ordinaire.
12.2.3 Chaque compartiment contenant des couchettes doit avoir au moins un extincteur à poudre chimique de 1 kg .
12.2.4 À côté de chaque appareil de cuisson, il doit y avoir au moins un extincteur à mousse de 4,5 L ou un extincteur à poudre chimique de 1 Kg .
12.2.5 Lorsque les compartiments utilisés pour l’ordinaire, dormir ou cuisiner sont contigus, les exigences concernant les extincteurs spécifiées aux paragraphes 12.2.2 et 12.2.4 doivent être satisfaites comme s’il s’agissait de compartiments distincts. Les appareils de lutte contre l’incendie équivalents doivent être évalués individuellement. Lorsque les zones réservées à l’ordinaire sont adjacentes aux compartiments machines, les parois de séparation doivent être imperméables aux gaz.
12.3 Endroits présentant un risque d’incendie
12.3.1 Les compartiments utilisés pour l’entreposage de matières inflammables comme de la peinture ou de l’huile doivent être pourvus d’un type de détecteur de fumée certifié à alarme sonore; le détecteur doit être certifié pour l’utilisation dans l’environnement dangereux où il peut être exposé.
12.3.2 Il doit y avoir au moins un extincteur à mousse de 9 L ou un extincteur polyvalent de type A, B ou C équivalent à tous les 15 mètres, immédiatement à côté de l’entrée de tout compartiment dans lequel des matières inflammables sont entreposées, et il doit être installé à un endroit bien en évidence (voir le tableau ci-après pour connaître les équivalences concernant les extincteurs).
12.3.3 Les surfaces intérieures des parois des compartiments dans lesquels des matières inflammables sont conservées doivent être construites selon la norme B-15.
12.3.4 Les surfaces exposées qui entourent les appareils de cuisson ou de chauffage doivent être faites d’un matériau incombustible ou doivent être protégées par un tel matériau.
12.3.5 Il faut prévoir au moins un extincteur à poudre chimique de 4,5 kg ou son équivalent par office/cuisine comportant des équipements pour préparer les repas.
12.3.6 Il faut prévoir un moyen pour évacuer à l'air libre les vapeurs provenant de la cuisine; il faut aussi prévoir des moyens permettant d'éliminer toute accumulation d’huile ou de graisse du conduit d'extraction. Le réseau de conduits de ventilation doit être doté d’un dispositif d’obturation étanche aux intempéries. Les conduits doivent être incombustibles et isolés là où ils traversent la structure.
Tableau 1: Équivalence des extincteurs
| Type | Eau ( L ) |
Mousse ( L ) |
Dioxyde de carbone ( kg ) | Poudre chimique ( kg ) |
|---|---|---|---|---|
| A | 9 | 9 | 2 polyvalente |
|
| B | 9 | 7 | 4,5 | |
| B | 46 | 16 | 9 | |
| B | 76 | 23 | 14 | |
| B | 151 | 45 | 23 | |
| C | 2 | 1 | ||
| C | 7 | 4,5 |
12.4 Compartiments machines
12.4.1 Les compartiments contenant des machines doivent comporter un dispositif de détection d’incendie faisant retentir une alarme sonore que l’on peut entendre de l’extérieur et également un signal visuel; le détecteur doit pouvoir être réarmé et doit comporter un dispositif d’essai.
12.4.2 Les compartiments contenant des machines doivent comporter un système d’extinction fixe qui peut être un extincteur portatif avec deux charges dont chacune est suffisante pour noyer le compartiment avec du dioxyde de carbone ou une substance extinctrice équivalente approuvée par TC . Il doit y avoir des dispositifs pour fermer les ouvertures qui pourraient laisser pénétrer de l’air dans de tels compartiments.
12.4.3 La décharge des extincteurs fixes doit être commandée à distance. La commande doit être dotée d’un dispositif de sécurité sûr, clairement étiquetée, et située à un poste de commande.
12.4.4 L'agent d'extinction pour systèmes fixes doit être entreposé dans des contenants solidement arrimés et bien identifiés à l’extérieur du compartiment protégé. Ces contenants doivent comporter un moyen d’indication positive du contenu sauf dans le cas des systèmes au CO2 car la pression ne permet pas une telle indication. Tous les systèmes doivent être recertifiés chaque année.
12.4.5 Nonobstant les exigences de la section 12.4.3, il faut également prévoir un dispositif de déclenchement manuel si le dispositif principal de l’agent d'extinction est électrique.
12.4.6 Lorsque le bateau est en bois, il faut traiter les surfaces du compartiment moteur exposées avec un revêtement ininflammable de peinture intumescente ou l’équivalent.
12.4.7 Lorsque le bateau est en plastique renforcé de fibres de verre, il faut incorporer des additifs ininflammables à la couche de résine exposée à l’intérieur du compartiment moteur ou, encore, la couche finale de la coque doit être en roving. Si l’une ou l’autre de ces deux opérations n’a pas été effectuée, on peut accepter l’application d’une peinture intumescente comme protection équivalente.
12.4.8 Il faut isoler toute paroi des compartiments machines adjacente aux locaux habités ou aux itinéraires d'évacuation au moins selon la norme B-15 et, sur les nouveaux voiliers-écoles, de tels espaces doivent être imperméables aux gaz.
12.4.9 Tout équipement électrique installé dans un compartiment machines doit être protégé et logé dans une enceinte pour empêcher la projection d’étincelles.
12.4.10 Les traversées des parois des compartiments machines ne doivent pas réduire la sécurité-incendie de ces parois.
12.5 Circuits d'alimentation et compartiments de stockage
12.5.1 Le mazout utilisé dans les installations fixes doit avoir un point d’éclair d’au moins 60 °C (essai en vase clos). Il est recommandé que les soutes soient situées à l’extérieur des compartiments machines et soient en acier.
12.5.2 Chaque conduite de carburant traversant une paroi d’un compartiment machines doit être pourvue d’une vanne d’arrêt commandée à distance, installée sur le réservoir, ou, lorsque cela n’est pas possible, d’une vanne d’arrêt à action rapide clairement identifiée située immédiatement à l’extérieur du compartiment machines, pour assurer un accès rapide à ces vannes en tout temps.
12.5.3 Il faut réduire au minimum les réserves d’essence que l’on doit transporter pour les moteurs des embarcations de secours. Il faut arrimer fermement le réservoir à essence sur le pont supérieur, loin de tout espace de travail habituel, et poser une affiche à cet effet.
12.5.4 Les compartiments à essence doivent être en laiton, en bronze, en plastique ou en tout autre matériau qui ne produira pas d’étincelles et qui est imperméable à l’essence.
12.5.5 Les réservoirs utilisés pour entreposer l’essence doivent être conformes à une norme approuvée par la CSA .
12.5.6 Les réservoirs à essence portatifs doivent être arrimés de façon que, lorsqu’ils sont pleins, ils soient retenus en place à des angles de gîte allant jusqu’à 60 degrés et sous des charges correspondant à une accélération de 2 g .
13. Équipement de sauvetage et de secours
13.1 Embarcations de sauvetage
13.1.1 Les bateaux doivent transporter des embarcations de sauvetage qui peuvent être des canots et des radeaux de sauvetage, pneumatiques ou à coque rigide, ou une combinaison des deux.
13.1.2 Le nombre d’embarcations de sauvetage et leur capacité doivent être suffisants pour le nombre total de personnes à bord. En outre, si un des radeaux de sauvetage manque ou n'est pas utilisable, le nombre d'embarcations doit être suffisant pour accueillir tous les passagers.
13.1.3 Les dispositifs de fixation des embarcations de sauvetage doivent résister à des forces d’accélération allant jusqu’à 2 g , dans toutes les directions, quand le bateau gîte à un angle allant jusqu’à 60 degrés.
13.1.4 Les embarcations de sauvetage doivent pouvoir être mises à l'eau rapidement, sans devoir utiliser d’outils spéciaux; lorsque cela est nécessaire, le mode d’emploi des mécanismes de dégagement doit être clairement décrit au poste d’arrimage. Ces instructions doivent être sous forme de pictogrammes.
13.1.5 Chaque embarcation de sauvetage doit être munie d’une bosse d’une longueur et d’une résistance suffisantes pour la maintenir fermement le long du bateau, lorsque celui-ci gîte à un angle allant jusqu’à 60 degrés. Cette bosse doit être attachée au bateau en tout temps.
13.1.6 Les radeaux de sauvetage pneumatiques doivent être transportés dans des contenants approuvés, être dotés de dispositifs de largage automatiques et être arrimés de façon que le contenant puisse émerger librement sans que la structure du bateau, le gréement ou autres éléments de l’équipement ne lui fassent obstacle.
13.1.7 Les embarcations de sauvetage doivent être arrimées tout équipés, le gouvernail ou le timon embarqués; les avirons, les dames de nage ou l’équipement mobile doivent aussi être solidement arrimés et les moteurs, les réservoirs à essence et les batteries doivent être en place et prêts à être utilisés en cas d’urgence.
13.1.8 Le nom du navire et du port d'immatriculation doivent être inscrits en caractères d’au moins 75 mm de haut, de façon permanente et d’une couleur contrastant avec le fond, sur toutes les embarcations de sauvetage.
13.1.9 Les réservoirs à essence de secours pour les embarcations de sauvetage doivent être solidement arrimés, dans un compartiment clairement identifié, sur le pont; si le compartiment est fermé, il doit avoir un évent dont la sortie est éloignée de tout espace normalement réservé au travail ainsi que d’un écran de protection contre les éclairs. Toutes les embarcations doivent être dotées de bandes rétroréfléchissantes, conformément aux exigences de l’Office des normes générales du Canada.
13.1.10 Le compartiment du réservoir à essence de secours doit comporter un dispositif empêchant toute fuite de carburant.
13.2 Gilets de sauvetage
13.2.1 Les bateaux doivent être dotés de gilets de sauvetage approuvés par Transports Canada en nombre suffisant pour 125 % des personnes à bord.
13.2.2 Les gilets de sauvetage doivent être arrimés solidement dans des compartiments facilement accessibles et clairement identifiés. On doit inscrire le nom du navire et du port d’immatriculation sur les gilets de sauvetage.
13.2.3 Les compartiments des gilets de sauvetage doivent offrir une protection maximale contre les dommages mécaniques et les éléments. De plus, ils doivent se situer loin des endroits potentiellement dangereux.
13.3 Autre équipement de sauvetage
13.3.1 Les bateaux doivent être dotés d’au moins trois bouées de sauvetage approuvées par Transports Canada.
13.3.2 Au moins une bouée de chaque côté doit être munie :
- d’un sifflet;
- d’un signal pyrotechnique de bouée de sauvetage et d’un signal fumigène qui s’active automatiquement;
- d’un signal pyrotechnique visible jour et nuit;
et au moins une autre bouée de sauvetage de chaque côté doit être munie d’un câble flottant d’au moins 30 mètres de longueur.
13.3.3 Les bouées de sauvetage doivent être disposées de façon que l’on puisse les larguer par le côté du bateau à l’aide d’un dispositif à déclenchement rapide. Elles doivent en outre être situées dans des compartiments facilement accessibles, situés près du côté du navire, tout en étant espacées à environ égale distance le long du pont, dans la zone de travail habituelle.
13.3.4 Les bateaux doivent être munis d’une perche pour récupérer une personne tombée à la mer.
13.3.5 Les bateaux doivent être munis d’un projecteur fixe ou portatif approprié pour procéder à la recherche de personnes tombées à la mer et aux opérations de récupération.
13.3.6 Les bateaux doivent être équipés d’une échelle de coque, d’un filet de sauvetage dépassant d’au moins 600 mm la ligne de flottaison ou de tout autre moyen permettant de retirer les personnes de l’eau ainsi qu’une élingue pour repêcher un corps d’au moins 100 kg.
13.3.7 Les bateaux doivent être munis d’au moins six fusées éclairantes de type A, B ou C et d’au moins six signaux de détresse de type A, B, C ou D transportés dans un compartiment flottant étanche aux intempéries installé sur le pont.
13.4 Équipement de secours
13.4.1 Les bateaux doivent être dotés d’au moins une trousse de premiers soins approuvée.
13.4.2 Les bateaux doivent être équipés d’un bassin oculaire situé, de façon stratégique, à côté de la zone d’entretien des batteries.
13.4.3 Les bateaux doivent être munis d’un ensemble de réparation de la voilure comprenant de la toile, du fil, une paumelle de voilier, des aiguilles, des pattes, des épissoirs et des poinçons à épisser appropriés aux voiles transportées.
13.4.4 Les bateaux doivent être dotés d’outils et de matériel qui peuvent être nécessaires pour couvrir ou réparer un dommage ou des fuites.
13.4.5 Les bateaux doivent être munis de moyens pour réparer l’appareil à gouverner, y compris un timon de secours ou son équivalent.
13.4.6 Les bateaux doivent être dotés de l’équipement requis pour couper les fils de fer en cas de démâtage.
14. Matériel de communication
14.1 Radiocommunication
14.1.1 Les bateaux doivent être conformes au Règlement sur les stations radio de navire ( RSRN ), tel que modifié, et au Règlement technique sur les stations de navires, ( RTSRN ) tel que modifié, ainsi qu’aux dispositions suivantes de la présente norme qui sont plus détaillées que ces règlements ou les complètent.
14.1.2 Les bateaux doivent être équipés d’au moins un radiotéléphone VHF permettant de transmettre et de recevoir sur la fréquence de 156,8 Mhz et les fréquences de communication maritimes appropriées au secteur d’opération. Les bateaux doivent par conséquent être conformes au Règlement sur les procédures et les règles de radiotéléphonie en VHF .
14.1.3 Les bateaux désirant opérer au-delà de la zone de rayonnement d’une station côtière VHF doivent posséder au moins un radiotéléphone Bhm capable de transmettre et de recevoir sur la fréquence de 2182 Khz et permettant d’effectuer une liaison bidirectionnelle entre le bateau et les stations côtières dans la bande FM .
14.1.4 Les bateaux doivent être munis d’au moins un radiotéléphone bidirectionnel VHF portatif que l’on peut utiliser s’il fallait les quitter. Les radiotéléphones VHF portatifs prévus à cette fin doivent être solidement arrimés et facilement accessibles de la position à laquelle on gouverne habituellement le bateau. Le radiotéléphone portatif doit être imperméable à l’eau (ou scellé dans un contenant imperméable à l’eau). Chaque radiotéléphone portatif doit posséder une batterie primaire spécialisée (comportant un sceau de sécurité indiquant qu’elle n’a pas encore été utilisée) qui ne doit servir qu’en cas d’urgence. Le radiotéléphone portatif doit pouvoir fonctionner sur le canal 16 de la fréquence VHF et sur au moins un autre canal.
14.1.5 Les bateaux devant naviguer en dehors des zones prévues pour les voyages de cabotage de classe IV ou des eaux secondaires, tel que définies dans le Règlement sur les voyages de cabotage, en eaux intérieures et en eaux secondaires, pour des périodes de plus de 24 heures, doivent être munis d’au moins une radiobalise de localisation des sinistres ( EPIRB ) de type 406 arrimée en un endroit où elle est protégée contre les dommages, prête pour une utilisation immédiate et être mise dans une embarcation de sauvetage. Elle doit être d’un type qui n’émerge pas librement en cas de naufrage. L’ EPIRB doit satisfaire aux exigences de la section 58.01 du RSRN .
14.1.6 Les antennes radiotéléphoniques doivent être dotées d’un dispositif de mise à la masse pour l’utilisation en cas d’orage électrique ou doivent être protégées par des paratonnerres ou d’autres moyens de protection.
14.2 Signaux visuels
14.2.1 Les bateaux doivent être munis d’une lampe de signalisation de jour pouvant fonctionner de façon indépendante du circuit électrique principal. La lanterne doit normalement être arrimée dans le poste de navigation principal.
14.2.2 Les bateaux doivent être dotés d’un ensemble de pavillons du code international de dimensions appropriées pour la signalisation.
15. Matériel de navigation
15.1 Généralités
15.1.1 Les bateaux doivent être conformes aux dispositions appropriées du Règlement sur les appareils et le matériel de navigation et du Règlement sur les cartes et les publications. Tous les bateaux doivent en outre être conformes aux dispositions de la présente norme qui ne sont pas traitées dans les règlements.
15.1.2 Les bateaux doivent être dotés d’un compas que l’on peut corriger et qui doit être situé dans un endroit permettant au timonier de voir facilement la rose des vents depuis le poste de gouverne principal. Le compas doit être muni d’un pelorus ou il doit être à relèvement manuel séparé.
15.1.3 Les bateaux doivent être dotés d’un dispositif électronique permettant de mesurer continuellement la profondeur de l’eau; en outre, il doit y avoir une sonde manuelle, portant les marques habituelles, d’au moins 20 brasses de longueur et comportant un plomb d’au moins 3,2 kg .
15.1.4 Les bateaux doivent avoir à bord la dernière édition corrigée et mise à jour des publications suivantes ayant trait à l’aire d’opération :
- cartes marines;
- tables des courants et des marées;
- liste des feux, des bouées et des signaux de brume;
- Instructions nautiques;
- Avis aux navigateurs;
- Aides radio à la navigation maritime;
- Signaux du code international;
- Code des pratiques maritimes;
- Normes relatives aux quarts.
15.1.5 Les bateaux que l’on prévoit utiliser hors de portée de vue des terres durant plus de 24 heures doivent être munis d’un sextant et d’un chronomètre ou d’un dispositif indicateur de temps efficace et, en plus des publications citées à la section 15.1.4, des éphémérides et des tables nautiques.
15.1.6 Il faut avoir toutes les données de correction appropriées pour tous les compas magnétiques sextants, chronomètres et indicateurs de temps à bord.
15.1.7 Il faut prendre des dispositions appropriées pour prévenir les dommages ou les risques d’incendie si la foudre venait à frapper les antennes ou les conducteurs du matériel de navigation.
15.1.8 Les bateaux doivent être équipés d’au moins un dispositif de positionnement mondial ( GPS ) et d’un système radar.
15.1.9 Les bateaux doivent être munis d’un journal de bord.
15.2 Feux, marques de signalisation et signaux sonores
15.2.1 Les bateaux doivent être conformes au Règlement sur les abordages ainsi qu’aux dispositions suivantes de la présente norme qui sont plus sévères que ces règlements ou les complètent.
15.2.2 Les bateaux doivent posséder des feux et des marques de jour, comme l’exige le Règlement sur les abordages, à savoir :
- deux feux rouges visibles sur tout l’horizon, près du sommet du mât le plus grand;
- un feu blanc visible sur tout l’horizon, dans le triangle avant.
Le jour, les feux exigés en a) et b) ci-dessus doivent être remplacés respectivement par deux boules noires et une boule noire.
15.2.3 Les feux exigés par le Règlement sur les abordages doivent être alimentés électriquement; de plus, on doit prévoir, si nécessaire, un deuxième ensemble de feux latéraux, de feux de poupe et de feux de tête de mât utilisant une autre source d’énergie, accompagné de dispositifs de fixation appropriés.
16. Ancres et chaînes
16.1 Les bateaux doivent être dotés de chaînes et d’au moins deux ancres à grande tenue, conformément au tableau des dimensions minimales ci-après. Les dimensions des ancres présentées dans le tableau concernent les ancres à grande tenue, c.-à-d. une ancre à pattes articulées, une ancre à soc de charrue, etc .
16.2 Les exigences présentées dans le tableau ci-après visent les yachts à voiles habituels. Lorsque ces bateaux présentent une prise au vent exceptionnellement élevée, en raison de leur important gréement ou de grosses superstructures, il faut augmenter le poids de chaque ancre de 25 %. Le calibre de la chaîne d’ancre doit être fonction du poids de l’ancre de dimension accrue.
16.3 Si l’ancre fournie est du type utilisé pour la pêche, le poids présenté dans le tableau doit être augmenté de 75 %, mais le calibre de la chaîne d’ancre demeure le même.
16.4 Chaque chaîne d’ancre doit être d’une longueur appropriée pour l’aire d’opération, mais la longueur ne doit en aucun cas être inférieure à 55 mètres pour l’ancre principale et l’ancre à jet. La chaîne de l’ancre principale doit être une chaîne véritable, tandis que celle de l’ancre à jet peut être une corde. Lorsque la chaîne d’ancre est une corde, il doit y avoir au moins 5 mètres de chaîne entre la corde et l’ancre. On doit prévoir au moins une ancre avec un cordage fixé en permanence dont l’extrémité extérieure doit se terminer par une chaîne et dont l’étalingure doit être arrimée en permanence au bateau.
16.5 Les bateaux doivent avoir une remorque dont le diamètre et la longueur sont au moins égaux à ceux de la chaîne de l’ancre à jet. La remorque peut être utilisée comme une aussière pour l’ancre à jet.
16.6 Lorsque le poids d’une ancre dépasse 50 kg , il faut prévoir un guindeau pour la manœuvrer.
16.7 Il doit y avoir un point d’arrimage solide sur le pont avant et un chaumard ou un rouleau à la proue qui peuvent être fermés sur la chaîne.
16.8 Il faut prévoir des moyens pour arrimer solidement chaque ancre lorsqu’elle est relevée.
16.9 Les bateaux doivent être équipés d’un dispositif de mouillage d’urgence qui ne requiert pas de source d’énergie.
Tableau 2 – Ancres et chaînes
| Longueur hors tout | Poids de l’ancre | Diamètre de la chaîne d’ancre | ||||
|---|---|---|---|---|---|---|
| Principale | à jet | Principal | à jet | |||
| Chaîne | Cordage | Chaîne | Cordage | |||
| (mètres) | ( kg ) | ( kg ) | ( mm ) | ( mm ) | ( mm ) | ( mm ) |
| Jusqu'à 9 | 15 | 8 | 8 | 12 | 6 | 10 |
| 10 | 17 | 9 | 8 | 14 | 8 | 12 |
| 11 | 20 | 10 | 8 | 14 | 8 | 12 |
| 12 | 23 | 12 | 8 | 14 | 8 | 12 |
| 13 | 26 | 13 | 9,5 | 16 | 8 | 12 |
| 14 | 30 | 15 | 9,5 | 16 | 8 | 14 |
| 15 | 24 | 17 | 9,5 | - | 8 | 14 |
| 16 | 28 | 19 | 11 | - | 8 | 14 |
| 17 | 44 | 22 | 11.... | - | 8 | 14 |
| 18 | 50 | 25 | 11 | - | 9,5 | 16 |
| 19 | 56 | 28 | 12,5 | - | 9,5 | 16 |
| 20 | 62 | 31 | 12,5 | - | 9,5 | 16 |
| 21 | 39 | 35 | 12,5 | - | 11 | 16 |
| 22 | 76 | 38 | 12,5 | - | 11 | 16 |
| 23 | 83 | 42 | 14 | - | 11 | 16 |
| 24 | 90 | 45 | 14 | - | 11 | 16 |
REMARQUES :
- Le diamètre de chaîne donné s’applique aux chaînes sans étai. Lorsque l’on utilise une chaîne étançonnée, le diamètre doit être modifié selon la force de rupture.
- Le diamètre du cordage donné s’applique aux cordages de nylon. Lorsque l’on utilise d’autres fibres, on doit modifier le diamètre selon la force de rupture.
- Lorsqu’une ancre à jet plus lourde est utilisée, le poids de l'ancre principale peut être réduit, pourvu que le poids combiné des deux ancres ne soit pas inférieur à 160 % du poids de l’ancre principale.
17. Divers équipements marins
17.1 Les bateaux doivent être dotés d’au moins deux bollards et de deux chaumards adjacents, de chaque côté du pont exposé.
17.2 Les bateaux doivent posséder un petit acastillage capable d’accepter une aussière pour remorquer le bateau.
17.3 Il faut installer un inclinomètre sur l’axe central du bateau, dans le poste de gouverne, au poste de contrôle ou dans la chambre des cartes ou, encore immédiat à côté.
17.4 Les bateaux doivent avoir un anémomètre fixe ou portatif.
17.5 Les bateaux doivent avoir un baromètre.
17.6 Des jumelles doivent se trouver à bord de tous les bateaux.
18. Emménagements
18.1 Locaux habités
18.1.1 Dans tous les bateaux conçus pour naviguer de nuit, il doit y avoir une couchette et un espace de rangement facilement accessible pour des vêtements secs et des effets personnels pour chaque personne à bord.
18.1.2 Les couchettes peuvent être superposées, pourvu qu’elles aient un dégagement vertical de 600 mm . Il est recommandé que le chevauchement des couchettes ne dépasse pas 60 % pour les couchettes ayant un faible dégagement vertical.
18.1.3 Chaque couchette doit être conçue pour pouvoir fixer une planche ou une toile de retenue anti-chute.
18.1.4 Chaque couchette doit être située dans le voisinage immédiat d’une planche d’embarquement ou d’un itinéraire d'évacuation.
18.1.5 Les couchettes peuvent être remplacées par des hamacs, pourvu qu’ils ne gênent pas les mouvements de façon importante; il faut prévoir des compartiments de rangement appropriés pour les hamacs.
18.1.6 Les locaux habités situés sous le pont exposé doivent comporter au moins deux itinéraires d'évacuation, dont au moins une doit mener directement au pont.
18.1.7 Il est recommandé que les itinéraires d'évacuation conduisant au pont exposé à partir des locaux habités soient situés aussi loin que possible d’une source d’incendie potentielle et aussi près que possible de l’axe central longitudinal.
18.1.8 Aucun compartiment situé dans la partie avant correspondant à 5% de la longueur de la ligne de flottaison, mesurée à partir de l’étrave, ne doit être utilisé comme local habité.
18.1.9 Il faut prévoir des moyens adéquats pour l’accrochage et le rangement des vêtements mouillés et ce, autant que possible dans des compartiments qui ne sont habituellement pas conçus pour être habités.
18.1.10 Les locaux habités doivent être éclairés et ventilés de façon adéquate; toutes les ouvertures qui peuvent être utilisées pour l’aération doivent comporter des dispositifs d’obturation efficaces; il faut pouvoir fermer de façon étanche aux intempéries les ouvertures pratiquées dans le pont exposé; les écoutillons latéraux doivent également pouvoir être fermés de façon étanche à l’eau.
18.1.11 Les locaux habités doivent comporter des contenants à déchets adéquats.
18.2 Toilettes et lavabos
18.2.1 Il faut prévoir au moins une salle de toilettes pour chaque groupe de 15 personnes à bord; les salles de toilettes doivent être complètement encloisonnées et comporter une ventilation assurant au moins dix changements de volume d’air par heure.
18.2.2 Toutes les toilettes doivent être d’un type marin approuvé; lorsque l’on utilise l’eau de mer pour la chasse d’eau, la prise d’eau de mer doit être immédiatement adjacente à la toilette et munie d’un robinet ou d’une vanne d’arrêt à la hauteur du passage de coque.
18.2.3 Il faut prévoir au moins un lavabo pour chaque groupe de 15 personnes à bord; toute prise d’eau de mer doit comporter un robinet ou une vanne d’arrêt à la hauteur du passage de coque adjacent au lavabo.
18.2.4 Toutes les eaux d’égout et eaux grises doivent être correctement acheminées vers leurs caissons de rétention respectifs (voir la section 8) si la loi l’exige.
18.3 Cuisines
18.3.1 Les bateaux conçus pour des voyages de nuit doivent être dotés d’une cuisine comprenant des installations de cuisson et d’entreposage des aliments avec régulation de température appropriée, une aire de préparation des aliments et une aire de lavage de la vaisselle.
18.3.2 Les appareils de cuisson, les appareils frigorifiques et les appareils de chauffage peuvent être à combustion, mais il est interdit d'utiliser l’essence ou l'électricité. Le combustible liquide ou gazeux doit provenir soit d’un réservoir d’entreposage en vrac à distance, soit d’un réservoir d’entreposage local d'une capacité maximale de 2 L (liquide) ou 500 grammes (gaz).
18.3.3 Les réservoirs d’entreposage en vrac de combustible pour la cuisson doivent approvisionner la cuisine au moyen de tuyaux bien assujettis et dont le parcours, autant que possible, évite les autres locaux habités. Les passages de cloison ou de pont doivent être munis de presse-étoupe pour réduire au minimum les frottements. La tuyauterie et les appareils utilisant du gaz de pétrole liquéfié ( G.P.L. ) ou du gaz naturel comprimé à des fins de cuisson doivent au moins satisfaire aux normes de la National Fire Protection Association ( NFPA ) ou de l’American Boat & Yacht Council.
18.3.4 Les cuisinières peuvent comporter des articulations ou des violons qui peuvent être immobilisés lorsque le bateau est à quai. Les raccords des conduites de combustible doivent être conçus pour compenser tout mouvement. Les cuisinières doivent comporter des violons pour assurer une protection adéquate contre tout déversement accidentel.
18.3.5 Lorsqu'un combustible gazeux est utilisé, il faut protéger la cuisine au moyen d’un détecteur de vapeurs, convenablement situé, qui émet une alarme sonore et actionne une vanne d’arrêt au point d’entreposage.
18.3.6 Il faut entreposer le combustible gazeux dans un compartiment donnant directement sur l’extérieur dans des contenants approuvés et protégés adéquatement contre les charges correspondant à une accélération de 2 g , à des angles de gîte pouvant aller jusqu’à 60 degrés. Lorsqu'il y a plusieurs contenants, ils doivent être raccordés à une conduite d’alimentation commune par l’intermédiaire de vannes d’isolement situées immédiatement en aval des contenants.
18.3.7 L’installation d'un système à combustibles gazeux doit être effectuée par un technicien certifié par l’Association canadienne du gaz.
18.3.8 Les installations d’entreposage des aliments et de cuisson doivent être arrimées adéquatement. Il faut prévoir des moyens de retenue des aliments ou des contenants capables de résister à des charges correspondant à une accélération de 2 g , à des angles de gîte pouvant aller jusqu’à 60 degrés.
18.3.9 La cuisine doit comporter une ventilation et le réseau de conduits de ventilation doit comporter un dispositif d’obturation étanche aux intempéries. Les conduits doivent être incombustibles et isolés à la hauteur des passages de la structure.
18.3.10 Les cuisines doivent comporter un nombre d’extincteurs approprié de dimensions et de type adéquats, mais qui, en aucun cas, inférieurs à un extincteur de 4,5 litres de type approprié.
19. Protection de personnel
19.1 Généralités
19.1.1 La surface du pont de travail doit être antidérapante. Les surfaces acceptables sont : le bois non peint; une texture antidérapante moulée dans du plastique renforcé de fibres de verre; un pont recouvert de peinture antidérapante ou recouvert d’un revêtement antidérapant. Il faut porter une attention particulière aux couvercles d’écoutille installés sur le pont de travail ainsi qu’aux côtés de toit inclinés utilisés comme pont de travail, qui peuvent présenter un risque accru quand le bateau est incliné.
19.1.2 Il doit y avoir un cale-pied d’au moins 25 mm de hauteur sur le périmètre du pont de travail.
19.2 Pavois et rambardes
19.2.1 Les périmètres des ponts exposés doivent être munis de pavois, de rambardes ou de câbles de protection d’une résistance et d'une hauteur suffisantes.
19.2.2 En général, il faut installer, tout autour du pont, des rambardes doubles tendues dont le câble ou la main courante se trouve à au moins 600 mm de hauteur. Ces rambardes doivent être supportées à des intervalles n’excédant pas 2,2 m .
19.2.3 Si l’arrière du poste de navigation s’ouvre sur la mer, des rambardes supplémentaires doivent être installées afin qu’il n’y ait pas d’ouverture verticale supérieure à 500 mm .
19.2.4 Un balcon doit être installé à l’avant de l’étai. Il doit avoir au moins la même hauteur que les rambardes, sauf dans le cas d’un beaupré très important où un filet approprié doit être installé.
19.2.5 Il doit y avoir suffisamment de mains courantes et de rampes à l’intérieur des emménagements, y compris les escaliers et les panneaux de descente des accès, pour permettre des déplacements sans danger en tout temps d’un compartiment à l’autre.
19.3 Ceintures de sécurité
19.3.1 Il faut prévoir une ceinture de sécurité pouvant rapidement être attachée ou détachée des lignes de sécurité pour chaque personne à bord.
19.3.2 Des cordages spéciaux, arrimés solidement au pont supérieur, doivent être en place pour servir de ligne de sécurité par mauvais temps; ils doivent être d’une longueur suffisante pour aller de l’avant à l’arrière, le long du pont, de chaque côté de l’aire normale de travail.
19.3.3 Il faut prévoir des dispositifs capables de retenir adéquatement les lignes de sécurité situées sur le pont découvert afin de fournir le maximum d’aide pour le déplacement de l’équipage, tout en évitant le plus possible d’obstruer les écoutilles et les embarcations de sauvetage ou d’empêcher la manipulation des gréements courants.
19.3.4 Il faut prévoir des points d’attache pour les ceintures de sécurité aux endroits suivants :
- près d’une descente;
- des deux côtés du poste de contrôle.
19.3.5 Il faut prévoir des moyens efficaces d’attacher les lignes des ceintures de sécurité sur les ponts exposés.
19.3.6 Les bateaux doivent comporter des mains courantes sur les côtés et aux extrémités des roufs.
19.4 Systèmes anti-chutes
19.4.1 Les personnes qui travaillent dans la mâture doivent porter un baudrier complet approuvé et recevoir une formation pour l’utiliser adéquatement.
19.4.2 Le point d’attache (anneau en D) ne doit pas être situé au-dessous du centre de gravité de la personne.
19.4.3 Les cordons attachés aux baudriers pour le travail dans les hauteurs ne doivent pas dépasser trois pieds de long, ou l’équivalent en unités métriques, sauf s’ils sont dotés d’un absorbeur d’énergie.
19.4.4 Les cordons et les mousquetons doivent être homologués par la CSA ou d’un type équivalent ou supérieur à ces normes de sécurité.
19.4.5 Pour les travaux exécutés sur le pont, les harnais de sécurité sont acceptés.
19.4.6 Les mâts et les espars sur lesquels les membres de l’équipage peuvent avoir à travailler dans le cours normal des opérations doivent être dotés de points d’attache pour les dispositifs anti-chute.
19.4.7 Il faut prévoir un dispositif anti-chute pour chaque membre de l’équipage devant travailler à plus de 2 m au-dessus du pont exposé.
19.4.8 Les étais et le matériel utilisés doivent pouvoir supporter toutes les charges en cause.
19.4.9 Il faut prévoir des points d’attache pour permettre aux personnes de traverser de façon sécuritaire les haubans des sections longitudinales lorsqu’ils sont attachés.
19.5 Consignes de sécurité
19.5.1 Le capitaine d’un voilier-école transportant des stagiaires doit s’assurer que chaque stagiaire :
- reçoit, le plus tôt possible après qu’il a rejoint le bateau pour la première fois, un enseignement théorique conçu pour le familiariser avec l’aménagement du bateau;
- reçoit, le plus tôt possible après qu’il a rejoint le bateau et, par la suite, à des intervalles ne dépassant pas une semaine, une formation sur les consignes de sécurité, notamment l’utilisation du matériel de lutte contre l’incendie et de sauvetage du bateau.
Annexe A: Specimen - Livret d'information sur la stabilite
A1 Renseignements généraux
- Nom du bateau
- Numéro officielNote de bas de page 1
- Port d’immatriculation Note de bas de page 1
- Nom et adresse du propriétaire
- Classe Note de bas de page 2
- Constructeur
- Date du début de la construction
- Dimensions
Longueur hors tout, y compris le beaupré
mètres
Longueur
mètres
Longueur à la ligne de flottaison
mètres
Largeur maximale
mètres
Creux Note de bas de page 3
mètres
Déplacement à pleine charge
mètres
Tirant d’eau à pleine charge Note de bas de page 4
tonnes
Franc-bord minimal
mètres
Jauge brute Note de bas de page 2
mètres
A 2 Ordre des sections
Ce livret est divisé en sections qui traitent les sujets les plus importants en premier.
Section 1 – Renseignements opérationnels
Cette section renferme des lignes directrices qui permettent de juger du niveau de stabilité en fonction d’un angle de gîte stable maximal recommandé pour prévenir l’envahissement par le haut en cas de rafales.
Section 2 – Données techniques et conditions de chargement
Cette section expose en détails les conditions de chargement d’après lesquelles on établit les angles de gîte recommandés.
Section 3 – Renseignements de base
Cette section renferme des renseignements de base nécessaires à l’exécution des calculs indiqués aux sections 1 et 2. Le capitaine n’a pas à consulter cette partie, mais l’échelle de Beaufort et la table de conversion des mesures métriques/impériales peuvent se révéler utiles
Section 1 - Renseignements opérationnels
A 3.1 Disposition des réservoirs et des ballasts
Figure 4 : emplacement des réservoirs
DWL : ligne de flottaison nominale
USK : partie inférieure de la quille
- Réservoir de carburant (bâbord)
- Réservoir de carburant (tribord)
- Réservoir d’eau douce
- Réservoir d’eau douce
- Réservoir des eaux-vannes
- Quille à ballast de plomb (18 tonnes)Note de bas de page 1
- Les tirants d’eau sont exprimés en fonction d’un prolongement de la partie inférieure de la quille
- Tous les autres points verticaux sont exprimés en fonction de la BASE Note de bas de page 2
- Tous les points longitudinaux sont exprimés en fonction de la MI-LONGUEURNote de bas de page 3
- L’assiette se définit comme : tirant d’eau arrière – tirant d’eau avant
- L’assiette nominale = inclinaison de la quille = 1,10 mètre
A 3.2 Plan de la voilure
| Voile | Surface en m² | Hauteur du centre de gravité au-dessus de la base, en m |
|---|---|---|
| 1. Foc n° 1 | 125 | 13,2 |
| 2. Foc n° 2 | 70 | 11,7 |
| 3. Voile d'étai | 45 | 10,2 |
| 4. Grand-voile | 100 | 13,1 |
| 5. Artimon | 40 | 10,3 |
| 6. Tourmentin | 27 | 8,2 |
| 7. Voile goélette | 28 | 9,6 |
Figure 5: plan de voilure
A 3.3 Angles d’immersion et d’envahissement par le livet
Table 2 : angles d’immersion et d’envahissement par le livet
| Description | Surface de l’ouverture, | Angles d'immersion | |
|---|---|---|---|
| en m² | 100 % de produits consomptibles degrés |
10 % de produits consomptibles degrés |
|
| Livet | -- | 24 | 27 |
| Descente principale | 0,80 | 84 | 89 |
| Descente avant | 0,65 | 92 | 97 |
| Claire-voie arrière | 0,11 | 63 | 70 |
| Claire-voie avant | 0,11 | 52 | 57 |
| Ventilation de la cuisineNote de bas de page 4 | 0,01 | 45 | 47 |
Un envahissement critique se produit lorsque les bords inférieurs des ouvertures ayant une surface combinée (en m² ) plus grande que
(le déplacement (en tonnes) / 1500) sont immergés
C’est-à-dire (65 / 1500) = 0,04 m²
L’immersion de la sortie d’air de la cuisine n’est donc pas considérée comme critique. C’est l’immersion de la claire-voie avant qui détermine l’angle critique d’envahissement par le haut mentionné dans ce livret.
Le capitaine doit prendre note que la sortie d’air et les claires-voies réduisent beaucoup la capacité du bateau à résister à l’envahissement par le haut. Aussi, lorsque ces ouvertures sont bien fermées, la sécurité du bateau est accrue de manière importante.
A 3.4 Notes sur la stabilité à l’intention du capitaine
- Le respect des critères de stabilité indiqués dans ce livret n’élimine pas tous les risques de chavirement et n’exempte pas le capitaine de ses responsabilités. Les capitaines doivent donc faire preuve de prudence et démontrer de bonnes connaissances de matelotage en ce qui concerne la saison de l’année, l’expérience des membres d’équipage, les prévisions météorologiques et la zone de navigation. En outre, ils doivent prendre les mesures appropriées en ce qui a trait au réglage de la vitesse et du cap ainsi qu’à l’établissement de la voilure selon les conditions dominantes.
- Avant d’entreprendre un voyage, il faut s’assurer que les grosses pièces d’équipement sont arrimées de manière adéquate pour réduire au minimum les risques de déplacements longitudinaux et transversaux attribuables aux effets des accélérations causées par le tangage et le roulis ou dans le cas d’une inclinaison à 90 degrés.
- En cas de conditions défavorables, de rafales, de lames déferlantes ou de bourrasques, toutes les portes, écoutilles, claires-voies et sorties d’air exposées doivent être fermées et attachées pour empêcher l’entrée d’eau. Il faut fabriquer et installer des fargues, etc.
- La quantité de voilure emportée est laissée à la discrétion du capitaine. Sa décision devra tenir compte de bon nombre de facteurs. Lorsque le capitaine évalue les risques d’envahissement par le haut, il doit s’aider des figures 6 et 7.
- La figure 6 indique l’angle de gîte stable maximal recommandé pour éviter que ne se produise un envahissement par le haut en cas de rafale. Le fait de naviguer avec un bateau à un angle de gîte plus élevé peut causer un envahissement par le haut si le bateau venait à rencontrer la plus forte rafale possible dans le courant d’air turbulent dominant. Cette situation peut provoquer un moment d’inclinaison transversal égal à deux fois celui du vent moyen.
- La figure 7 indique l’angle de gîte stable maximal recommandé pour prévenir l’envahissement par le haut en cas de rafale. Le fait de naviguer avec un bateau à un angle de gîte plus élevé peut causer un envahissement par le haut si le bateau venait à subir les effets de gîte d’une bourrasque provenant d’un noyau orageux ou d’un système de fronts. Cette situation peut entraîner un moment d’inclinaison transversal bien supérieur à celui du vent moyen. Pour cette raison, le capitaine doit prendre en considération les courbes d’angles de gîte stables maximaux attribuées pour une plage de vitesses de coups de vent.
- À l’aide des valeurs indiquées par l’inclinomètre et l’anémomètre, le capitaine peut déterminer le degré du risque de chavirement en cas de rafale ou de bourrasque qui peuvent être causées par le système météorologique dominant. À ce moment, il peut décider de diminuer la voilure et de prendre d’autres mesures qu’il estime nécessaire.
- Il faut également faire bien attention lorsque l’on navigue avec vent arrière car, en cas de rafale venant frapper de travers, les effets de gîte attribuables au vent peuvent atteindre un niveau dangereux si l’angle de gîte précédent était faible.
3.5 Angle de gîte stable maximal pour prévenir l’envahissement par le haut en cas de rafale
Figure 6: Angle de gîte stable maximal, rafales
Rafales
Lorsque le bateau navigue par vent soutenu, il gîte à l’angle correspondant au point d'intersection de la courbe du bras de levier de gîte et de la courbe GZ. Lorsqu’une rafale frappe le bateau, l’angle de gîte s’accroît à l’intersection de la courbe du bras de levier de gîte par rafale et de la courbe GZ. Le moment d’inclinaison transversal augmente proportionnellement au carré de la vitesse apparente du vent.
Si le bateau navigue à un angle de gîte moyen inférieur à 27°, les ouvertures susceptibles d’être envahies par le haut de manière importante ne seront pas immergées à la plus forte rafale du courant d’air turbulent dominant. Cette situation peut provoquer un moment d’inclinaison transversal égal à deux fois celui du vent moyen (c’est-à-dire que la vélocité du vent apparent moyen a augmenté de 1,4).
A 3.6 Courbes de l’angle de gîte stable maximal pour prévenir l’envahissement par le haut par rafales
Figure 7 : Angle de gîte stable maximal, rafales
Rafales
Les courbes de l’angle de gîte stable maximal indiquent la fourchette d’angles de gîte stables ou moyens au-delà desquels le bateau est envahi par le haut en cas de rafale.
Si le bateau navigue dans un cyclone, notamment dans l’obscurité, où des rafales violentes sont imminentes, l’angle de gîte stable maximal recommandé doit être réduit proportionnellement à la vitesse du vent apparent moyen, conformément aux courbes indiquées ci-dessus.
A 3.7 Exemples de l’utilisation des courbes de l’angle de gîte stable maximal
Figure 8 : courbes de l’angle de gîte stable maximal
Exemple A
Le voilier est barré aux allures portantes et la vitesse du vent apparent soutenu est de 16 nœuds. L’angle de gîte moyen est de 15 degrés. Les prévisions et les cumulonimbus laissent entrevoir la possibilité de rafales. Les tracés de l’angle de gîte et de la vitesse du vent (point A, figure 8) indiquent que le bateau risque de gîter à l’angle d’envahissement par le haut à des rafales de 30 nœuds. Pour être plus à l’abri d’un envahissement par le haut, à savoir résister à des rafales allant jusqu’à 45 nœuds, il faut diminuer la voilure ou arriser pour réduire l’angle de gîte moyen à 7 degrés (point A1, figure 8) ou moins.
Exemple B
Le voilier louvoie et la vitesse du vent apparent est de 30 nœuds. L’angle de gîte moyen est de 20 degrés. On ne prévoit pas de rafales. L’angle de gîte est sensiblement inférieur à 27 degrés (angle de gîte stable maximal recommandé). Il existe donc une marge de sécurité adéquate contre un envahissement par le haut en cas de forte rafale. Les tracés des valeurs relatives à la vitesse du vent et à l’angle de gîte (point B, figure 8) indiquent aussi que le bateau n’est pas sujet à un envahissement par le haut en cas de rafale, à moins que celles-ci ne frappent à une vitesse supérieure à environ 50 nœuds. Il n’est donc pas nécessaire d’amener les voiles pour assurer la stabilité du bateau.
Section 2 - Données techniques et conditions de chargement
A 4.1 Marques de franc-bord
Figure 9 : marques de franc-bord
Creux depuis la partie inférieure de la quille jusqu’à la partie supérieure du pont en bois, à mi-longueur du bateau
3,88 mètres
Tirant d’eau maximal à pleine charge, à mi-longueur du bateau
2,72 mètres
Franc-bord minimal à mi-longueur du bateau
1,16 mètre
A 4.2 Capacité des réservoirs
Table 3 : capacité des réservoirs
| Réservoir | Capacité m³ |
Poids tonnes |
CGL mètres à l’avant |
CGV mètres au-dessus de la base |
MCL tonnes.m |
|---|---|---|---|---|---|
| Carburant B | 1,06 | 0,92 | -2,4 | 2,03 | 0,13 |
| Carburant T | 1,06 | 0,92 | -2,4 | 2,03 | 0,13 |
| Réservoir d’eau douce (Arrière) | 0,70 | 0,70 | -7,0 | 2,30 | 0,10 |
| Réservoir d’eau douce (Avant) | 1,12 | 1,12 | -0,2 | 1,03 | 0,56 |
| Réservoir des eaux-vannes | 0,80 | 0,80 | 2,1 | 1,11 | 0,24 |
A 4.3 Condition 1 : départ à pleine charge
Table 4 : produits consomptibles à pleine charge
| Nom de l’élément | Poids tonnes |
CGL mètres |
MOML tonnes |
CGV mètres |
MOMV tonnes |
MCL tonnes |
|---|---|---|---|---|---|---|
| Réservoir à carburant (bâbord) | 0,92 | -2,400 | -2,21 | 2,030 | 1,87 | 0,1 |
| Réservoir à carburant (tribord) | 0,92 | -2,400 | -2,21 | 2,030 | 1,87 | 0,1 |
| Réservoir d’eau douce (arrière) | 0,70 | -7,000 | -4,90 | 2,300 | 1,61 | 0,1 |
| Réservoir d’eau douce (avant) | 1,12 | -0,200 | -0,22 | 1,030 | 1,15 | 0,6 |
| Réservoir des eaux-vannes | 0,08 | 2,100 | 0,17 | 0,700 | 0,06 | 0,0 |
| Approvisionnements | 1,00 | 0,000 | 0,00 | 2,500 | 2,50 | 0,0 |
| Équipage et effets | 1,80 | 0,000 | 0,00 | 3,600 | 6,48 | 0,0 |
| Marge de croissance | 2,80 | 0,000 | 0,00 | 3,880 | 10,86 | 0,0 |
| Port en lourd | 9,34 | -1,003 | -9,37 | 2,826 | 26,40 | 0,9 |
| Bateau lège | 56,04 | -0,311 | -17,43 | 2,234 | 125,19 | 0,0 |
| Déplacement | 65,38 | -0,410 | -26,80 | 2,319 | 151,59 | 0,9 |
Tirant d’eau arrière
3,339 m
Tirant d’eau avant
2,094 m
Tirant d’eau moyen
2,717 m
Assiette
1,246 m à l’arrière
Distance métacentrique (sans carène liquide)
1,424 m
GM corrigé pour carène liquide
1,410 mètres
Courbe de stabilité pour la condition 1
Figure 10 : courbe de stabilité à pleine charge
Condition 2 : arrivée avec 10 % de produits consomptibles
Table 5 : poids et déplacement-arrivée avec 10% de produits consomptibles
| Nom de l’élément | Poids tonnes |
CGL mètres |
MOML tonnes |
CGV mètres |
MOMV tonnes |
MCL tonnes |
|---|---|---|---|---|---|---|
| Réservoir à carburant (bâbord) | 0,09 | -2,400 | -0,22 | 1,500 | 0,14 | 0,0 |
| Réservoir à carburant (tribord) | 0,09 | -2,400 | -0,22 | 1,500 | 0,14 | 0,0 |
| Réservoir d’eau douce (arrière) | 0,07 | -7,000 | -0,49 | 1,900 | 0,13 | 0,0 |
| Réservoir d’eau douce (avant) | 0,11 | -0,200 | -0,02 | 0,700 | 0,08 | 0,0 |
| Réservoir des eaux-vannes | 0,70 | 2,100 | 1,47 | 1,000 | 0,70 | 0,2 |
| Approvisionnements | 0,10 | 0,000 | 0,00 | 2,500 | 0,25 | 0,0 |
| Équipage et effets | 1,80 | 0,000 | 0,00 | 3,600 | 6,48 | 0,0 |
| Marge de croissance | 2,80 | 0,000 | 0,00 | 3,880 | 10,86 | 0,0 |
| Port en lourd | 5,76 | -0,091 | 0,53 | 3,259 | 18,77 | 0,2 |
| Bateau lège | 56,04 | -0,311 | -17,43 | 2,234 | 125,19 | 0,0 |
| Déplacement | 61,80 | -0,274 | -16,90 | 2,330 | 143,97 | 0,2 |
Tirant d’eau arrière
3,208 m
Tirant d’eau avant
2,121 m
Tirant d’eau moyen
2,664 m
Assiette
1,087 m à l’arrière
Distance métacentrique (sans carène liquide)
1,395 m
GM corrigé pour carène liquide
1,391 m
Courbe de stabilité pour la condition 2
Figure 11 : courbe de stabilité avec 10% de produits consomptibles
Section 3 - Renseignements de base
A 5.1 Notes sur l’utilisation des moments de carène liquide
Si un réservoir est entièrement rempli de liquide, aucun mouvement de liquide n’est possible. Les effets sur la stabilité du bateau sont tout à fait identiques, les mêmes que si le réservoir contenait des matières solides.
Dès que l’on retire une quantité de liquide du réservoir, la situation change complètement. La stabilité du bateau est modifiée par ce que l’on appelle l’« effet de carène liquide ». Cet effet négatif sur la stabilité est désigné sous le nom de « perte de stabilité » ou de « hausse virtuelle du CGV ». On calcule cette perte de stabilité de la façon suivante :
Perte de stabilité due aux effets de carène liquide
= inertie de carène liquide (m4) x densité du liquide dans le réservoir ( tonnes/m³ ) / déplacement du bateau (tonnes)
= moment de carène liquide (tonne.m) / déplacement du bateau (tonnes)
Les moments de carène liquide énumérés au tableau « Capacité des réservoirs » s’appliquent à des réservoirs isolés. Si les réservoirs sont interreliés, les moments de carène liquide seront considérablement supérieurs. On doit donc laisser les vannes d’interconnexion fermées lorsque le bateau est en mer.
A 5.2 Tirant d’eau
Figure 12 : courbes hydrostatique
A 5.3 Tracé des courbes de stabilité
Figure 13 : courbes de stabilité
A 5.4 Notes sur l’utilisation des courbes de stabilité
Les courbes de stabilité pour des déplacements compris entre 25 et 75 tonnes sont données à intervalles pour les angles de gîte allant de 10 à 140 degrés. On suppose que la coque, le pont principal et les roufs fermés (voir la figure 14 ci-après) sont étanches à l’eau pour tous les angles de gîte.
On obtient les courbes du bras du levier de redressement ( GZ ) à un déplacement donné par l’équation suivante :
GZ = KN – KG.sin (angle de gîte)
(voir la figure 15 ci-après)
Cette équation permet de calculer la valeur de GZ à chaque angle de gîte. Par la suite, on peut tracer cette valeur selon les conditions de chargement indiquées.
Figure 14 : courbes du bras
A 5.5 Compte rendu de l’essai d’inclinaison
| Déviations | |||||
|---|---|---|---|---|---|
| No du poids | Direction des déplacements | Poids tonnes |
Distance mètres |
1 mm | 2 mm |
| 1 | > tribord | 0,3050 | 4,8600 | 33,00 | 31,00 |
| 2 | > tribord | 0,3050 | 4,8600 | 36,00 | 32,00 |
| 3 | > bâbord | 0,3050 | 4,8600 | 35,00 | 32,00 |
| 4 | > bâbord | 0,3050 | 4,8600 | 39,00 | 35,00 |
| 5 | > bâbord | 0,3050 | 4,8600 | 33,00 | 29,00 |
| 6 | > bâbord | 0,3050 | 4,8600 | 36,00 | 32,00 |
| 7 | > tribord | 0,3050 | 4,8600 | 34,00 | 32,00 |
| 8 | > tribord | 0,3050 | 4,8600 | 36,00 | 31,00 |
Longueurs de pendule (en mètres)* :
1)2,115 2) 1,960
Valeurs du tirant d’eau, de l’avant à la mi-longueur, au-dessus de la ligne de quille :
Position (mètres): -8,800
Tirant d’eau (mètres): 3,240
Position (mètres): 8,800
Tirant d’eau (mètres): 2,040
Densité de l’eau 1,0210
En position inclinée
* une longueur de pendule est acceptable pour les bateaux de moins de 24 mètres.
Note de bas de page:
Il faut présenter une description générale de l'essai portant notamment sur le personnel responsible, la procédure et l'équipement utilisés, les conditions dominantes et les précautions àcautions à prendre pour s'assurer de l'exactitude de l'essai.
L'inclinaison d'un voilier doit se faire par des conditions où il y a peu ou pas de vent en raison de la prise importante du gréement dans le vent.
Éléments à enlever pour calculer le poids du bateau lège
| Nom de l’élément | Poid tonnes |
CGL mètres |
CGV mètres |
MCL tonnes. m |
|---|---|---|---|---|
| Carburant (bâbord) | 0,92 | -2,400 | 2,030 | 0,00 |
| Carburant (tribord) | 0,92 | -2,400 | 2,030 | 0,00 |
| Eau douce (avant) | 1,12 | -0,020 | 1,030 | 0,00 |
| Outils de l’électricien | 0,07 | -4,000 | 1,600 | 0,00 |
| Poids d’inclinaison | 1,22 | 0,800 | 3,750 | 0,00 |
| Équipage | 0,23 | 0,000 | 3,000 | 0,00 |
Éléments à ajouter pour calculer le poids du bateau lège
| Nom de l’élément | Poids tonnes |
CGL mètres |
CGV mètres |
MCL tonnes.m |
|---|---|---|---|---|
| Ancre et chaîne | 0,30 | 9,000 | 3,800 | 0,00 |
| Radeaux | 0,15 | -5,900 | 3,900 | 0,00 |
Conditions lèges
A 5.6 Vitesses et pressions correspondantes du vent sur l’échelle de Beaufort
Table 6 : pressions du vent
| Échelle de Beaufort | Description générale | Limites de vitesse en nœuds | Pression kg/m² |
|---|---|---|---|
| 1 | très légère brise | 1 à 3 | 0,02 – 0,2 |
| 2 | légère brise | 4 à 6 | 0,3 – 0,6 |
| 3 | petite brise | 7 à 10 | 0,8 – 1,7 |
| 4 | jolie brise | 11 à 16 | 2,0 – 4,2 |
| 5 | bonne brise | 17 à 21 | 4,8 – 7,3 |
| 6 | vent frais | 22 à 27 | 8 – 12 |
| 7 | grand frais | 28 à 33 | 13 – 18 |
| 8 | coup de vent | 34 à 40 | 19 – 26 |
| 9 | fort coup de vent | 41 à 47 | 27 – 37 |
| 10 | tempête | 48 à 55 | 38 – 50 |
| 11 | violente tempête | 56 à 63 | 52 – 66 |
| 12 | ouragan | 64 ou plus | 68 ou plus |
A 5.7 Conversion des mesures métriques/impériales
Table 7 :conversion des mesures métriques/impériales
| Multiplier par | Pour convertir des | En | |
|---|---|---|---|
| 0,039370 | millimètres | pouces | 25,400 |
| 0,39370 | centimètres | pouces | 2,5400 |
| 3,2808 | mètres | pieds | 0,30480 |
| 2,2046 | kilogrammes | livres | 0,45359 |
| 0,00098421 | kilogramme | tonnes (2 240 lb ) | 1016,0 |
| 0,98421 | tonnes métriques (1 000 k) | tonnes (2 240 lb ) | 1,0160 |
| 2,4999 | tonne par centimètre | tonnes par pouce | 0,40002 |
| 8,2017 | tonnes mètres ( M.C.T.C. ) | pieds tonnes ( M.C.T.I. ) | 0,12193 |
| 18798 | radians mètres | degrés pieds | 0,0053198 |
| Pour obtenir des | À partir de | Multiplier par |
- 10 mm³ = 1 cm³
- 1 cm³ Densité en douce 1,0 = 1 g
- 1 000 cm³ Densité en douce 1,0 = 1 k
- 1 m³ Densité en douce 1,0 = 1 t (1 000 k )
- 1 m³ Densité en salée 1,025 = 1,025 t
- 1 t Densité en salée 1,025 = 0,975 m³
- 1 m³ = 35,315 pi³
- 1 pi³ = 0,0283 m³
Figure 15 : courbes de stabilité prévenir l’envahissement par le haut en cas de coups de vent
A 5.8 Notes concernant la dérivation de l’angle de gîte stable maximal pour
HA1 = (GZ1 / cos1..3Θf)
où HA1 est la longueur du levier de gîte dû au vent à 0 degré qui fait gîter le bateau jusqu’à l’angle d’envahissement par le haut (Θf ou 60 degrés, selon la valeur la plus faible).
GZf est le levier de la courbe GZ du bateau à l’angle d’envahissement par le haut (Θf ) ou à 60 degrés, selon l’angle le plus faible.
HA2 est le bras de levier de gîte par vent moyen, peu importe l’angle (2 degré)
= 0,5 x HA1 x cos1,3Θ
A 5.9 Notes concernant la dérivation des courbes de l’angle de gîte stable maximal pour prévenir l’envahissement par le haut en cas de rafale
Le moment d’inclinaison transversal du vent est proportionnel à la pression du vent et au carré de la vitesse du vent apparent. Il est aussi fonction de la surface, de la hauteur, de la forme et de la cambrure des voiles, de la direction du vent apparent et du gradient du vent dominant. Lorsqu’un bateau gîte, le moment d’inclinaison transversal du vent diminue et, à n’importe quel angle (Θ) compris entre 0 (droit) et 90 degrés, il est relié à la valeur verticale par la fonction suivante :
HM = HM0 cos1,3Θ , où HM0 est le moment d’inclinaison transversal lorsque le bateau est vertical.
L’angle de gîte d’un bateau correspond à l’intersection de la courbe du bras de levier de gîte et de la courbe du bras du levier de redressement GZ , où HA = HM/déplacement.
Lorsque le bateau est exposé à une rafale ou à un coup de vent, il gîte à un angle supérieur au point d'intersection de la courbe du bras de levier de gîte correspondant à la vitesse de la rafale et de la courbe GZ .
Figure 16 : courbes de stabilité
Pour un angle donné, on peut donc déduire une courbe de bras de levier de gîte et, pour un changement donné de la vitesse du vent, on peut prédire le changement de l’angle de gîte résultant.
L’envahissement par le haut d’un bateau se produit au point d'intersection de la courbe du bras de levier de gîte et de la courbe GZ à l’angle d’envahissement par le haut. Le diagramme où la « courbe du bras de levier de gîte par rafale » recoupe la courbe GZ à 52° illustre cette situation. Si l’on part de l’hypothèse où la surface des voiles est suffisante pour faire gîter le bateau à l’angle d’envahissement par le haut (utiliser la valeur de 60 degrés si l’angle d’envahissement dépasse celle-ci) en cas de rafales de 45 nœuds par exemple, on peut alors prédire la vitesse du vent qui donnerait un angle de gîte plus faible dans ces circonstances. On calcule le bras de levier de redressement en cas de rafale ( HA1 ) par la formule suivante :
HA1 = ( GZf / cos1..3Θf)
Si l’on prend comme point de départ que l’angle de gîte stable est de 20 degrés avant la rafale, on peut, de la même façon, calculer la valeur correspondante du bras de levier de redressement ( HA2 ) :
HA2 = (GZ20 / cos1..320)
Le rapport HA2 /HA1 correspond au rapport des pressions du vent avant et pendant la rafale. En conséquence, pour une vitesse de vent (V1) de 45 nœuds qui donne lieu à un envahissement par le haut, on calcule la vitesse du vent avant la rafale (V2) qui donnerait un angle de gîte de 20 degrés par la formule suivante :
V2 = V1 racine carrée de
Dans cet exemple, qui est illustré dans le diagramme :
Θf= 52 degrés
GZf = 0,725 mètre
HA1 = 1,362 mètre
GZ20 = 0,464 mètre
HA2 = 0,503 mètre
D’où V2 = 27,4 nœuds
En conséquence, lorsque l’on navigue à une vitesse de vent apparent de 27,4 nœuds à un angle de gîte moyen de 20 degrés, une augmentation de la vitesse du vent apparent à 45 nœuds pour le même angle moyen de vent apparent cause un envahissement par le haut si l’on ne peut pas prendre des mesures pour diminuer le moment d’inclinaison transversal.
Ces valeurs correspondent à un point de la courbe de rafale de 45 nœuds indiquée à la page 10, qui a été calculée à partir d’une série d’opérations similaires à l’aide de différents angles de gîte stables. De la même façon, les courbes d’autres vitesses ont été déduites en utilisant diverses valeurs de V1.
On doit effectuer ces calculs dans le cas de conditions de chargement et de résultats correspondant à la pire éventualité (c’est-à-dire les angles de gîte stables maximaux les plus faibles) indiquée dans ce livret.