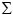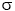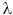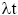CALCUL DES NIVEAUX D'ALERTE
Le but d'un niveau d'alerte est d'identifier les écarts significatifs par rapport à une norme de performances déjà établie. Le niveau ne doit pas être élevé au point qu'une augmentation importante de la fréquence des défaillances ne produise pas une alerte; inversement, il ne doit pas être bas au point qu'une distribu-tion normale des défaillances produise des alertes trop fréquemment. Par conséquent, la détermination du niveau d'alerte sera normalement basée sur la distribution ou "éparpillement" observé dans la fréquence des défaillances du système étudié.
Il existe plusieurs méthodes reconnues de calcul des niveaux d'alertes. Chacune d'elles peut être acceptable, à condition qu'elle soit définie entièrement dans le document de programme de l'exploitant. Les méthodes décrites dans les pages suivantes sont données à titre d'exemple; on peut en trouver beaucoup d'autres dans les livres traitant de statistiques.
Pour permettre la comparaison, les trois premiers exemples utilisent les mêmes données. On constatera que les niveaux d'alerte obtenus diffèrent légèrement selon la méthode utilisée; toutefois, ces petites différences ne sont pas considérées comme étant significatives. Grâce à un système efficace de présentation des données (voir annexe B), un niveau d'alerte mal choisi devrait apparaître clairement.
Les symboles utilisés dans la présente annexe auront les significations conventionnelles suivantes:
_
| x (x barré) | = moyenne d'un ensemble de données |
| N | = nombre de données |
| X | = valeur des données |
| (lettre grecque majuscule sigma) | somme d'un ensemble de données |
| (lettre grecque minuscule sigma) | écart type |
| (lettre grecque minuscule lambda) | nombre de défaillances |
| t (lettre grecque minuscule tau) | temps |
| (lambda tau) | = fréquence des défaillances |
EXEMPLE 1
Pireps -1.3 niveau d'alerte moyen
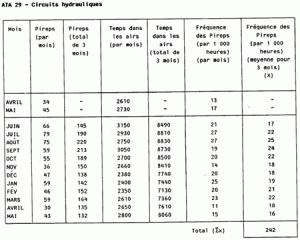
La moyenne pour trois mois de la fréquence Pirep par 1 000 heures pour chaque système (ou sous-système), comme au tableau de la figure 1 ci-contre, est répartie sur la période d'exploitation d'échantillonnage et porte le nom de moyenne (x); la moyenne est multipliée par 1.3 pour produire le niveau d'alerte d'un système donné.
Même si l'expérience a démontré que cette méthode était efficace dans le cas d'une distribution typique des défaillances, elle risque de produire des niveaux d'alerte excessifs dans le cas d'un système dont les fréquences de défaillances sont très irrégulières, et ne serait pas suffisamment sensible dans le cas de données présentant un faible éparpillement.
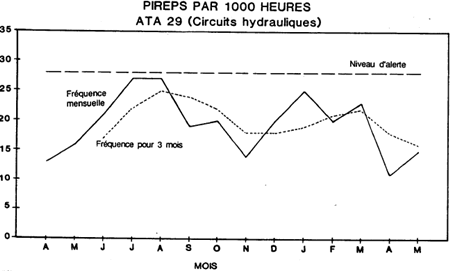
Dans l'exemple donné, le niveau d'alerte (26) serait dépassé pour les mois de juillet et d'août.
Figure 1
Pireps par 1 000 hrs
Nombre de données dans l'échantillon (N) = 12
Moyenne (x) =
x Niveau d'alerte = 1.3x
N
= 242 = 1.3 x 20
12
= 20 (arrondi) = 26
EXEMPLE 2
Pireps - 2
niveau d'alerte (calculé à l'aide d'une calculatrice)
La moyenne pour trois mois de la fréquence Pireps par 1 000 heures pour le système (ou sous-système) est répartie sur la période d'exploitation d'é-chantillonnage et porte le nom de moyenne (x) comme à l'exemple 1. L'écart type (la moyenne quadratique de la quantité par laquelle la donnée diffère de la moyenne) est calculé de la façon montrée, multiplié par 2 et addition-né à la moyenne pour produire le niveau d'alerte.
Même si dans l'exemple montré ci-contre le niveau d'alerte obtenu est le même que pour la méthode 1.3 x de l'exemple 1, cela n'est pas toujours le cas. Le niveau d'alerte 2s diffère de la méthode précédente en ce sens qu'il est plus sensible à la nature des données, et est particulièrement approprié aux données fortement éparpillées (c'est-à-dire les données ayant un écart type élevé).
Le niveau d'alerte 2s présente une probabilité de fausses alertes (provoquées par un écart de l'éparpillement normale) d'environ 4.5 %.
Dans l'exemple donné, le niveau d'alerte est obtenu à l'aide d'une calculatrice munie d'une fonction statistique. Les symboles des touches et l'ordre des opérations peuvent varier en fonction du type de calculatrice utilisée.
Étape 1:
Choisir le mode statistique: INV (2e fonction) MODE (stat ou "SD")
Étape 2: Effacer: INV SAC (effacer statistiques)
Étape 3: 17 M+ 22 M+ 25 M+ 24 M+ 22 M+ 18 M+ Entrer les données:
19 M+ 21 M+ 22 M+ 18 M+ 16 M+
Étape 4: touche affichage
Obtenir les résultats: Nombre de (N) n 12
données
Total (
x)
x 242
Moyen terme (x) x 20.16666667
Écart type (
)
n 2.763853995
Étape 5:
Niveau d'alerte = 2 x 2.763853995 + 20.16666667 = 25.69437466
Arrondi à 26
EXEMPLE 3
Pireps -niveau d'alerte 3
La moyenne, plus 3 écarts types comme le montre la figure 3 ci-contre. 3
est probablement le niveau d'alerte le plus utilisé.
Le niveau d'alerte 3
convient particulièrement bien aux données à faible éparpillement (c'est-à-dire les données ayant normalement un faible écart type); la probabilité de fausses alertes avec cette méthode est de 0.3 %.
Contrairement aux méthodes précédentes, avec les données d'échantillonnage choisies, le niveau d'alerte 3
ne produit pas d'alerte pour les mois de juillet et d'août. Vous trouverez ci-dessous un graphique des données utilisées dans l'exemple.
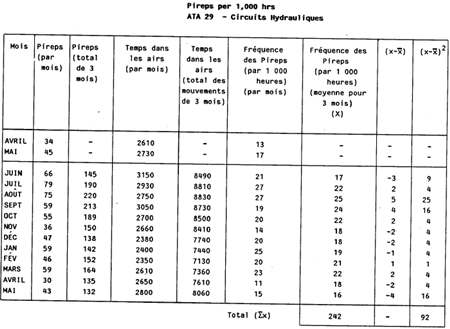
Figure 3
Nombre de données dans l'échantillon (N) = 12
Moyenne (x) =
x Écart type (s) =
(x-x)2
N N
= 242 = 92
12 12
= 20 (arrondi) = 7.67
= 2.77
Niveau d'alerte = Moyenne (x) + 3
= 20 + (3 x 2.77)
= 28.31 arrondi à 28
5h
EXEMPLE 4
Déposes non prévues de composants -méthode Poisson
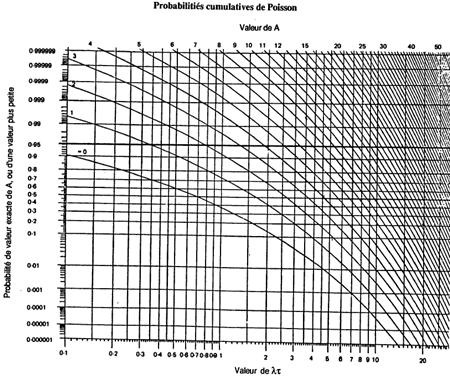
La surveillance de composants particuliers nécessitent soit un plus grand nombre d'éléments, soit un niveau d'expérience plus élevé que pour la surveillance de systèmes complets. L'exemple suivant est basé sur une expérience de 21 mois, et fournit un niveau d'alerte pouvant être utilisé comme période de comparaison de 3 mois. Avec un plus grand nombre d'éléments, (soit un plus grand nombre d'appareils, soit un plus grand nombre de composants par appareil), les périodes nécessaires pour l'expérience et la comparaison peuvent être réduites. Le niveau d'alerte est établi à une probabilité cumulative de 95 % calculée à l'aide de l'abaque des probabilités cumulatives de Poisson de la page suivante, comme le montre les deux exemples suivants:
(a) Composant: Amplificateur de tangage du pilote automatique
Nombre de composants par aéronef n = 1
Nombre de déposes non prévues des 21 derniers mois N = 62
Utilisation de la flotte au cours des 21 derniers mois H = 36840
Heures de fonctionnement du composant au cours des 21 derniers mois T = (n x H) = 36840
Utilisation de la flotte au cours des 3 mois courants h = 5895
Heures de fonctionnement du composant au cours des 3 mois courants t = (n x h) = 5895
Nombre de déposes non prévues au cours des 3 mois courants x = 12
Fréquence moyenne de déposes non prévues, = N = 0.00168
T
Nombre probable de déposes non prévues au cours des = 0.0168 x 5895
3 mois courants, = 9.9 arrondi à 10 (
)
À l'aide de la figure 4, en entrant dans l'abaque au point
= 10 l'intersection avec 0.95 (probabilité de 95 %) nous donne le nombre maximal acceptable de déposes non prévues de composants (la valeur A) pour la période de 3 mois; ce nombre est 15.
En comparant ce nombre à la valeur courante de x qui est de 12, on se rend compte qu'il n'existe pas de "situation d'alerte" pour ce composant.
(b) Composant: Vanne de régulation de température
Nombre de composants par aéronef n = 3
Nombre de déposes non prévues des 21 derniers mois N = 31
Utilisation de la flotte au cours des 21 derniers mois H = 36840
Heures de fonctionnement du composant au cours de 21 derniers mois T = (n x H) = 110520
Heures de fonctionnement du composant au cours des 3 mois courants h = 5895
Utilisation de la flotte au cours des 3 mois courants t = (n x h) = 17685
Nombre de déposes non prévues au cours des 3 mois courants x = 9
Fréquence moyenne de déposes non prévues, = 31 = 0.00028
110520
Nombre probable de déposes non prévues au cours des 3 mois courants, = 0.00028 x 17685
= 5.01 arrondi to 5 (lt)
D'après l'abaque, la valeur acceptable de A est de 8.
Comme la valeur courante de x est de 9, on a donc dépassé le niveau d'alerte dans ce cas.
Figure 4